【G検定】t-SNE

t-SNE

t-SNEとは

t-SNEとは、高次元データの可視化に適している次元削減アルゴリズムです。名前は、t-distributed Stochastic Neighbor Embedding (t 分布型確率的近傍埋め込み) を表します。

考え方は、点の間の類似度が反映されるように高次元の点を低次元に埋め込む、というものです。線形では表現できない関係も学習して次元削減を行える利点があります。

具体的には、高次元空間での点同士の近さを確率分布で表し、それと低次元空間での点同士の近さを確率分布で表したものとの差異を最小化するように学習します。このアルゴリズムは可視化に特化しており、PCAなどと比較してより複雑なデータでも有効に働きやすいです。

t-SNEの特徴

・高次元データを2次元や3次元に落とし込むための次元削減アルゴリズムです。
・高次元空間での点同士の近さを確率分布で表し、それと低次元空間での点同士の近さを確率分布で表したものとの差異を最小化するように学習します。
・高次元データの局所的な構造 (類似しているデータを低次元上でも近くに保つこと) を非常によく捉えるだけでなく、大局的な構造 (異なるクラスタやスケール) も可能な限り保った可視化ができる点が特徴です。
・可視化に特化しており、PCAなどと比較してより複雑なデータでも有効に働きやすいです。
・手書き数字や画像認識などの高次元データを可視化する際によく用いられます。また、生物学や医学などの分野でも応用されています。

t-SNEのアルゴリズム

・t-SNEは、高次元空間での点同士の近さを確率的に表し、それと低次元空間での点同士の近さを確率的に表したものとの違いを小さくすることで、次元削減を行います。
・高次元空間での点同士の近さを表す確率分布は正規分布 (ガウス分布) を使いますが、低次元空間での点同士の近さを表す確率分布はt分布 (スチューデント分布) を使います。
・高次元空間での点同士の近さを表す確率分布において、正規分布の幅 (分散) を調整するパラメーターがあります。このパラメーターはPerplexityと呼ばれ、データセットや目的に応じて適切な値に設定する必要があります。
・高次元空間での点同士の近さと低次元空間での点同士の近さとの違いを測る指標としてKLダイバージェンス (カルバック・ライブラー ダイバージェンス) を使います。KLダイバージェンスは非対称な指標なため、高次元空間で近い点が低次元空間では遠くなる場合は大きなペナルティがかかりますが、逆に高次元空間で遠い点が低次元空間では近くなる場合はあまりペナルティがかかりません。
・最初にランダムに配置された低次元空間上の点を少しずつ動かしてKLダイバージェンスを小さくするように学習します。この学習方法は勾配法と呼ばれます。

t-SNEの実用例

t-SNEの実用例として、以下のようなものがあります。
・画像データ: 画像データはピクセル数や色数などで高次元になりがちです。t-SNEでは画像データをベクトル化して2次元に変換して可視化しました。その結果、画像の内容や特徴に応じてクラスターが形成されました。
・音声データ: 音声データは周波数や振幅などで高次元になりがちです。t-SNEでは音声データをベクトル化して2次元に変換して可視化しました。その結果、音声の言語や話者に応じてクラスターが形成されました。
・テキストデータ: テキストデータは単語や文書などをベクトル化した高次元データです。t-SNEではテキストデータを2次元に変換して可視化しました。その結果、テキストの意味やトピックに応じてクラスターが形成されました。

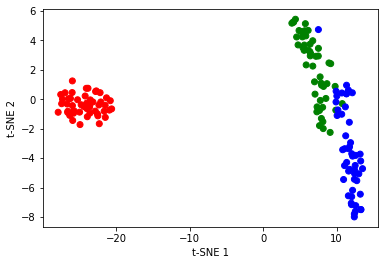
t-SNEの実装

# データセットの読み込み
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data # 特徴量
y = iris.target # クラスラベル

# t-SNEのインポート
from sklearn.manifold import TSNE

# t-SNEのインスタンス作成
tsne = TSNE(n_components=2, perplexity=30, random_state=0)

# 高次元データを低次元に変換
X_tsne = tsne.fit_transform(X)

# プロット用に色分け
import numpy as np
colors = np.array(["red", "green", "blue"])
y_colors = colors[y]

# matplotlibでプロット
import matplotlib.pyplot as plt
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y_colors)
plt.xlabel("t-SNE 1")
plt.ylabel("t-SNE 2")
plt.show()

t-SNEは高次元データのクラスター構造や類似性を低次元空間でも保持することができるため、データの分布や特徴を視覚的に理解することができます。