このシリーズではE資格対策として、書籍「ゼロから作るDeep Learning」を参考に学習に役立つ情報をまとめています。
<参考書籍>
ニューラルネットワークの概要
パーセプトロンからニューラルネットワークへ
パーセプトロンは、1958年にフランク・ローゼンブラットが提案した最も初期のニューラルネットワークの一種です。パーセプトロンは、複数の入力を受け取り、それらの入力に対応する重みを掛け合わせた結果を閾値と比較して、出力を決定します。この単純な構造は、線形分類問題を解決することができましたが、非線形問題には適用できませんでした。
その後、1980年代に発展したニューラルネットワークは、複数のパーセプトロンを層状に重ねることで、より複雑な非線形問題に対応できるようになりました。この多層構造は、入力層、隠れ層、出力層から構成され、層ごとに多数のニューロンが存在します。ニューロン間の結合には、重みが設定され、学習によって最適化されます。
ニューラルネットワークとは
ニューラルネットワーク(Neural Network, NN)は、人間の脳の神経回路を模倣した機械学習の一手法です。ニューラルネットワークは、複雑なパターンや非線形な関係を持つデータを処理する能力があり、画像認識、自然言語処理、ゲームプレイなど、多様なタスクで高い性能を発揮します。
ニューラルネットワークの基本構造は以下のようになります。
- 入力層(Input Layer): データの特徴量が入力される最初の層です。各特徴量は、個々のニューロン(またはノード)に対応します。
- 隠れ層(Hidden Layer): 入力層と出力層の間にある層で、一つまたは複数の隠れ層が存在することがあります。隠れ層のニューロンは、前の層からの入力に重みをかけ、バイアスを加えた後、活性化関数を適用して出力を生成します。
- 出力層(Output Layer): ネットワークの最後の層で、タスクに応じた予測結果が出力されます。出力層のニューロン数は、問題の種類によって異なり、回帰問題では1つ、多クラス分類問題ではクラス数に等しくなります。
ニューラルネットワークの学習方法
ニューラルネットワークの学習は、主に以下の手順で行われます。
- 重みの初期化: ネットワークの重みをランダムな値に設定します。これは学習の出発点となります。
- 順伝播(Forward Propagation): 入力データを入力層から出力層へと伝播させ、予測値を計算します。各層で活性化関数を適用し、非線形性を導入します。
- 損失関数の計算: 予測値と実際のラベルとの差を計算し、ネットワークの性能を評価します。損失関数は、回帰問題では平均二乗誤差、分類問題では交差エントロピー損失などが一般的です。
- 誤差逆伝播(Backpropagation): 損失関数の勾配(微分)を計算し、出力層から入力層へと逆向きに伝播させます。これにより、各ニューロンの重みとバイアスに対する損失関数の勾配が計算されます。
- 重みの更新: 勾配降下法(Gradient Descent)や確率的勾配降下法(Stochastic Gradient Descent, SGD)、Adamなどの最適化アルゴリズムを用いて、重みとバイアスを更新します。更新された重みとバイアスにより、次の学習サイクルが開始されます。
- 収束: 重みとバイアスの更新が繰り返され、損失関数の値が十分に小さくなると、学習が収束したとみなされます。学習率、収束条件、最大エポック数(学習の反復回数)などのハイパーパラメータは、学習プロセスの効率や性能に影響を与えます。
ニューラルネットワークは、その構造や活性化関数、損失関数、最適化アルゴリズムなどの要素を組み合わせてカスタマイズすることができます。これにより、さまざまな問題やデータセットに対応できる柔軟性が得られます。ただし、過学習や勾配消失、勾配爆発といった問題に対処するために、正則化、ドロップアウト、バッチ正規化などのテクニックが必要となることがあります。
活性化関数
活性化関数は、ニューラルネットワークの各ニューロンで用いられる関数で、ニューロンの出力を決定する役割を持ちます。活性化関数の導入によって、ニューラルネットワークは非線形性を獲得し、より複雑な問題に対応できるようになりました。活性化関数は、ニューロンの入力に対して何らかの変換を行い、その結果を次のニューロンに渡します。
活性化関数の目的
活性化関数は、主に以下の2つの目的で使用されます。
- 非線形性の導入: 活性化関数によって、ニューラルネットワークは線形問題だけでなく、非線形問題にも対応できるようになります。これにより、表現力が向上し、現実の複雑な問題に対処できるようになります。
- 勾配の伝播: 活性化関数は、誤差逆伝播法において、勾配を伝播させるためにも重要な役割を果たします。適切な活性化関数が選択されることで、学習中に勾配消失や勾配爆発といった問題を回避し、効率的な学習が可能になります。
活性化関数の代表例
いくつかの代表的な活性化関数を紹介します。
- ステップ関数: パーセプトロンで使用される関数で、閾値を超えると1を出力し、それ以外では0を出力します。非線形性は導入されますが、微分不可能なため、誤差逆伝播法での学習には適用できません。
- シグモイド関数: 入力された値を0から1の範囲に変換する関数です。非線形性が導入され、微分可能であるため、誤差逆伝播法での学習に適用できます。ただし、入力の絶対値が大きい場合、勾配が非常に小さくなるため、勾配消失問題が発生することがあります。
- 双曲線正接関数 (tanh): 入力された値を-1から1の範囲に変換する関数で、シグモイド関数の改良版とも言えます。非線形性が導入され、微分可能であり、勾配消失問題はシグモイド関数よりも緩和されています。
- ReLU (Rectified Linear Unit): 入力が0より大きい場合、入力値をそのまま出力し、0以下の場合は0を出力する関数です。非線形性が導入され、計算コストが低く、勾配消失問題も起こりにくいため、ディープニューラルネットワークではよく使用されます。ただし、入力が負の場合、勾配が0になるため、勾配消失問題が発生することがあります。
- Leaky ReLU: ReLUの改良版で、入力が負の場合でも微小な勾配を持つようになっています。これにより、勾配消失問題が緩和されています。
これらの活性化関数以外にも、多くの種類が存在し、問題やニューラルネットワークの構造に応じて適切な活性化関数を選択することが重要です。
活性化関数の実装
ステップ関数
パーセプトロンで使用される関数で、閾値を超えると1を出力し、それ以外では0を出力します。
# NumPyライブラリをnpとしてインポート
import numpy as np
# matplotlibのpylabモジュールをpltとしてインポート
import matplotlib.pylab as plt
# ステップ関数を定義
def step_function(x):
# xが0より大きい場合は1、そうでない場合は0を要素とするNumPy配列を返す
return np.array(x > 0)
# -5.0から5.0まで0.1刻みのNumPy配列を生成
X = np.arange(-5.0, 5.0, 0.1)
# ステップ関数にXを入力してYを計算
Y = step_function(X)
# XとYをプロット
plt.plot(X, Y)
# y軸の表示範囲を-0.1から1.1までに指定
plt.ylim(-0.1, 1.1)
# グラフを表示
plt.show()実行結果:

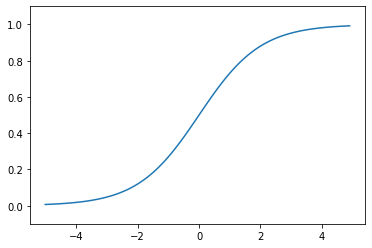
シグモイド関数
入力された値を0から1の範囲に変換する関数です。非線形性が導入され、微分可能であるため、誤差逆伝播法での学習に適用できます。
# NumPyライブラリをnpとしてインポート
import numpy as np
# matplotlibのpylabモジュールをpltとしてインポート
import matplotlib.pylab as plt
# シグモイド関数を定義
def sigmoid(x):
# シグモイド関数の計算式を返す
return 1 / (1 + np.exp(-x))
# -5.0から5.0まで0.1刻みのNumPy配列を生成
X = np.arange(-5.0, 5.0, 0.1)
# シグモイド関数にXを入力してYを計算
Y = sigmoid(X)
# XとYをプロット
plt.plot(X, Y)
# y軸の表示範囲を-0.1から1.1までに指定
plt.ylim(-0.1, 1.1)
# グラフを表示
plt.show()実行結果:
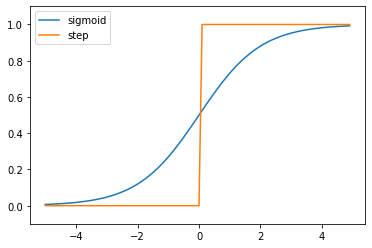
ステップ関数とシグモイド関数の比較
ステップ関数とシグモイド関数を比較し、それぞれの特徴と違いについて考察でしてみます。
# NumPyライブラリをnpとしてインポート
import numpy as np
# matplotlibのpylabモジュールをpltとしてインポート
import matplotlib.pylab as plt
# シグモイド関数を定義
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# ステップ関数を定義
def step_function(x):
return np.array(x > 0)
# -5.0から5.0まで0.1刻みのNumPy配列を生成
x = np.arange(-5.0, 5.0, 0.1)
# シグモイド関数にxを入力してy1を計算
y1 = sigmoid(x)
# ステップ関数にxを入力してy2を計算
y2 = step_function(x)
# xとy1をプロットし、ラベルに'sigmoid'を設定
plt.plot(x, y1, label='sigmoid')
# xとy2をプロットし、ラベルに'step'を設定
plt.plot(x, y2, label='step')
# y軸の表示範囲を-0.1から1.1までに指定
plt.ylim(-0.1, 1.1)
# 凡例を表示
plt.legend()
# グラフを表示
plt.show()実行結果:
結果をまとめると以下のようになります。
このコードを通じて、ステップ関数とシグモイド関数を比較し、それぞれの特徴と違いについて考察できます。
- ステップ関数は、閾値(ここでは0)を境にして出力が急激に切り替わる関数です。つまり、入力が0より大きい場合は1を、それ以外の場合は0を出力します。この特徴から、ステップ関数はバイナリ(2値)分類問題に適していると言えます。
- 一方、シグモイド関数は、入力が大きくなると1に近づき、入力が小さくなると0に近づくS字型のカーブを描く関数です。シグモイド関数は連続的で微分可能であり、出力が0から1の範囲内に収まるため、確率を表現するのに適しています。
- ステップ関数は非連続的であり、微分ができないため、勾配降下法などの最適化アルゴリズムを用いた学習が難しいです。一方、シグモイド関数は微分可能であり、勾配情報を利用した学習が可能です。
- ステップ関数は、出力が0か1のいずれかであるため、ニューラルネットワークの活性化関数として用いた場合、中間層の出力が非常にシンプルになります。しかし、シグモイド関数は出力が連続的であるため、より複雑な表現が可能です。
これらの考察から、ステップ関数とシグモイド関数はそれぞれ異なる特徴を持ち、問題やニューラルネットワークの設計によって適切な関数を選択することが重要です。現在の深層学習では、シグモイド関数やReLU(Rectified Linear Unit)関数などの連続的で微分可能な活性化関数が一般的に利用されています。
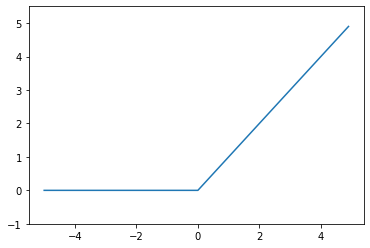
ReLU関数
入力が0より大きい場合、入力値をそのまま出力し、0以下の場合は0を出力する関数です。
# NumPyライブラリをnpとしてインポート
import numpy as np
# matplotlibのpylabモジュールをpltとしてインポート
import matplotlib.pylab as plt
# ReLU関数を定義
def relu(x):
# 0とxのうち大きい方の値を返す
return np.maximum(0, x)
# -5.0から5.0まで0.1刻みのNumPy配列を生成
x = np.arange(-5.0, 5.0, 0.1)
# ReLU関数にxを入力してyを計算
y = relu(x)
# xとyをプロット
plt.plot(x, y)
# y軸の表示範囲を-1.0から5.5までに指定
plt.ylim(-1.0, 5.5)
# グラフを表示
plt.show()実行結果:
まとめ
最後までご覧いただきありがとうございました。
