このシリーズではE資格対策として、書籍「ゼロから作るDeep Learning」を参考に学習に役立つ情報をまとめています。
<参考書籍>
隠れ層のアクティベーション分布
ニューラルネットワークの各層における活性化値(アクティベーション)の分布は、そのネットワークの学習状況や設計の良さを示す重要な指標となります。
まず、活性化関数とは何かを理解することから始めましょう。活性化関数は、ニューラルネットワークの各層で計算された値(線形変換の結果)に適用され、その結果を次の層へと伝えます。この活性化関数により、ニューラルネットワークは非線形の関係性も学習することができます。よく使われる活性化関数にはReLU(Rectified Linear Unit)、シグモイド関数、tanh(ハイパボリックタンジェント)などがあります。
そして、各層での活性化値の分布を見ることで、以下のような問題を検出することができます。
- 勾配消失問題(Vanishing Gradient Problem): 活性化関数としてシグモイド関数やtanhを用いた場合、出力がその関数の最大値または最小値に近い値に集中すると、その値の勾配がほぼ0になる問題が発生します。つまり、活性化値の分布が0や1(シグモイドの場合)、-1や1(tanhの場合)に偏っていると、この問題が起こっている可能性があります。この問題が発生すると、学習が進行するにつれて勾配が消失し、ネットワークのパラメータが更新されなくなるため、学習が停滞します。
- 発散する活性化値: ReLUを活性化関数として使用した場合、重みの初期値が大きすぎると、活性化値が非常に大きな値になる可能性があります。これが発生すると、勾配が爆発し、学習が不安定になることがあります。
隠れ層のアクティベーション分布の比較
シンプルなニューラルネットワークの動作を模擬し、各隠れ層の出力の分布をヒストグラムとして描画するものです。
# numpyとmatplotlib.pyplotをインポートします。numpyは数値計算、matplotlibはグラフ描画のためのライブラリです。
import numpy as np
import matplotlib.pyplot as plt
# シグモイド関数を定義します。シグモイド関数は、非線形の活性化関数の一つで、出力を0から1の間に制約します。
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 1000 x 100 のランダムな入力データを生成します。np.random.randnは標準正規分布に従う乱数を生成します。
input_data = np.random.randn(1000, 100)
# 各隠れ層のノード(ニューロン)数を設定します。今回は100ノードとします。
node_num = 100
# 隠れ層の数を設定します。今回は5層とします。
hidden_layer_size = 5
# 各層の活性化の結果を保存するための辞書を初期化します。
activations = {}
# 入力データをxとします。
x = input_data
# 各隠れ層で行う処理をループします。
for i in range(hidden_layer_size):
# 2回目以降のループでは、前層の活性化の結果を次の層の入力とします。
if i != 0:
x = activations[i-1]
# 重みを初期化します。ここでは標準正規分布に従うランダムな値を用います。
w = np.random.randn(node_num, node_num) * 1
# 入力データと重みのドット積(行列積)を計算します。これが全結合層の基本的な操作です。
a = np.dot(x, w)
# 活性化関数としてシグモイド関数を適用します。
z = sigmoid(a)
# 活性化の結果を保存します。
activations[i] = z
# 各層の活性化の結果をヒストグラムで表示します。
for i, a in activations.items():
# subplotを使って、各層のヒストグラムを並べ
plt.subplot(1, len(activations), i+1)
# プロットのタイトルには、何層目のヒストグラムであるかを表示します。
plt.title(str(i+1) + "-layer")
# 2層目以降のヒストグラムでは、y軸の目盛りを非表示にします。
if i != 0: plt.yticks([], [])
# 活性化の結果をヒストグラムとしてプロットします。データはflatten()で1次元化し、ビンの数は30、範囲は0から1とします。
plt.hist(a.flatten(), 30, range=(0,1))
# 全てのヒストグラムを表示します。
plt.show()
以下に各部分の詳細な解説をします。
まず、numpyとmatplotlib.pyplotという2つのライブラリをインポートします。numpyは数値計算を助けるライブラリで、matplotlib.pyplotはグラフ描画のライブラリです。
次に、3つの活性化関数、すなわちsigmoid、ReLU、tanhを定義します。
sigmoid関数は、実数を入力として0から1の間の値を出力します。ニューラルネットワークでよく使われる活性化関数の一つです。ReLU(Rectified Linear Unit)関数は、入力が0未満ならば0を、それ以外ならば入力値をそのまま出力します。これもニューラルネットワークでよく使われる活性化関数です。tanh(ハイパボリックタンジェント)関数は、実数を入力として-1から1の間の値を出力します。これもニューラルネットワークで使われる活性化関数の一つです。
次に、ランダムな1000 x 100の行列を作成し、これをニューラルネットワークの入力データとしています。これは1000個の100次元のベクトルを作成しているとも考えられます。
その後、ノード(ニューロン)の数と隠れ層の数をそれぞれ100と5に設定し、各層の活性化を保存する辞書activationsを初期化します。
その後のforループでは、各隠れ層について処理を行っています。具体的には、前の層の出力(初めてのループでは入力データ)とランダムな重み行列とのドット積を計算し、その結果をシグモイド関数に通して次の層の入力(活性化)を得ています。この活性化はactivations辞書に保存されます。
最後に、各層の活性化のヒストグラムを描画しています。具体的には、各層の活性化を1次元に平坦化(flatten)し、その分布をヒストグラムとして描画しています。なお、2層目以降のヒストグラムではy軸の目盛りは表示されません。
重みの初期値を変えて比較してみる
上記の各隠れ層の出力の分布において、以下のように重みの初期値を変えて、比較を行います。
~~略~~
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
# 以下の4通りの初期値の比較を行う
w = np.random.randn(node_num, node_num) * 1
w = np.random.randn(node_num, node_num) * 0.01
w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)
a = np.dot(x, w)
~~略~~実行結果:
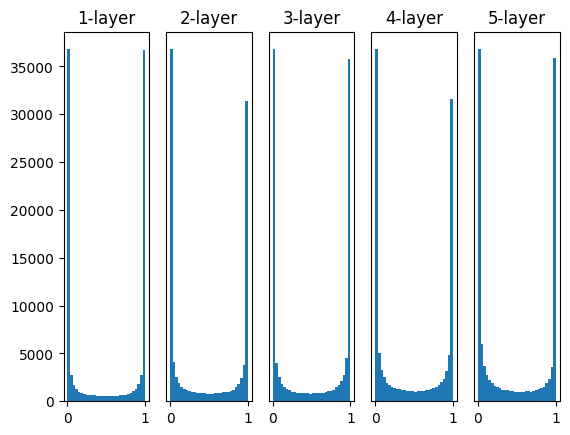
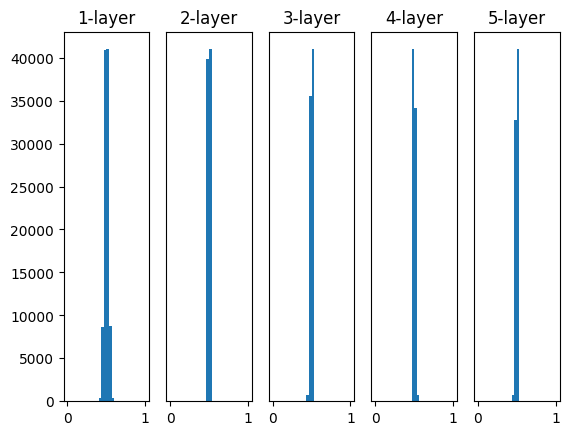
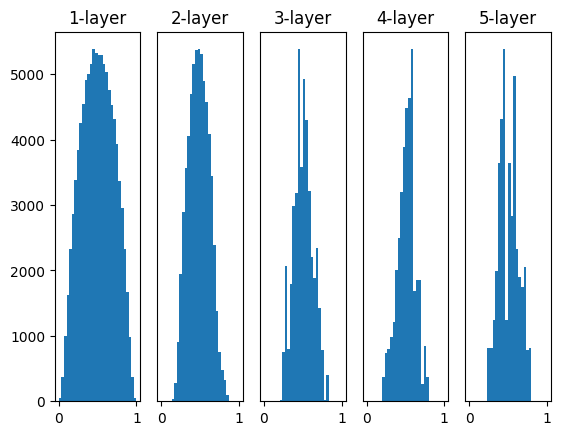
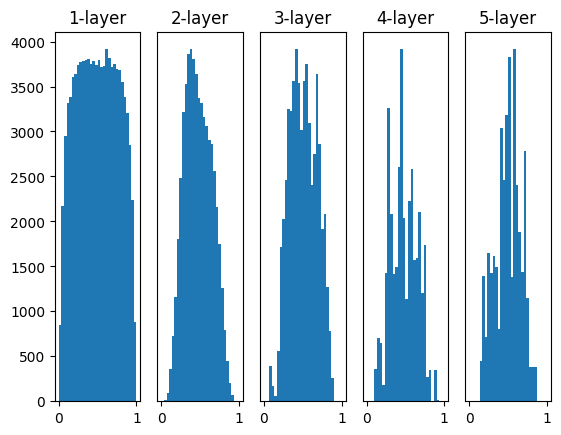
重みの初期値がネットワークの学習に大きな影響を及ぼすことはよく知られています。以下の4つの方法で重みの初期値を設定してみると、それぞれが学習にどのような影響を及ぼすかを視覚的に理解することができます。
w = np.random.randn(node_num, node_num) * 1:この設定では、標準正規分布から生成されたランダムな値が重みとして使用されます。しかし、この初期値設定は活性化出力の分布が偏る可能性があり、勾配消失もしくは爆発を引き起こす可能性があります。w = np.random.randn(node_num, node_num) * 0.01:この設定では、小さなランダムな値が重みとして使用されます。これは重みの値を小さくすることで、勾配消失や爆発を防ぐためのものですが、活性化出力が偏る可能性があります(特にシグモイド関数やtanh関数を使用した場合)。w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num):これは「Xavierの初期値」です。Xavierの初期値は、前の層のノード数の平方根でスケーリングされたランダムな値を重みとして使用します。これは活性化関数が線形(またはその近似)である場合に最適化されています。w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num):これは「Heの初期値」です。Heの初期値は、ReLU関数に最適化されています。前の層のノード数の平方根でスケーリングされたランダムな値を重みとして使用します。
まとめ
最後までご覧いただきありがとうございました。

