【G検定まとめ】要点整理＆当日用カンペの項目別詳解ページです。
詳細な知識や実装は試験には必ずしも必須ではありませんが、試験対策として理解を深めたい方はぜひ最後までご覧ください。
G検定まとめはこちら
線形回帰
回帰問題に用いる手法でシンプルなモデルの1つデータ（の分布）があったときに、そのデータに最も当てはまる直線を考える。線形回帰に正則化項を加えた手法として以下の方法がある。
線形回帰とは
線形回帰とは、説明変数に対して目的変数が線形またはそれから近い値で表される状態のことです。線形回帰は統計学における回帰分析の一種であり、非線形回帰と対比されます。線形回帰の目的は、説明変数と目的変数の間の関係を線形の式で表すことで、未知のデータから目的変数の値を予測することです。
線形回帰には単純線形回帰と重回帰の2種類があり、単純線形回帰は説明変数が1つの場合、重回帰は説明変数が2つ以上の場合に用いられます。
線形回帰の例
線形回帰の例としては、以下のようなものがあります。
・身長と体重の関係を線形の式で表す。
・広告費と売上の関係を線形の式で表す。
・愛の深さと結婚年数の関係を線形の式で表す。
これらの例では、説明変数と目的変数の間に線形の関係があると仮定して、データに最もよく当てはまる直線を求めています。この直線の式を使って、未知のデータから目的変数の値を予測することができます。
線形回帰のメリット・デメリット
線形回帰のメリットとデメリットは以下のようになります。
メリット
・説明変数と目的変数の関係がほぼ線形である場合に最適な結果が得られます。
・線形の式で表現できるため、解釈が容易です。
・計算量が少なく、実装が比較的簡単です。
デメリット
・外れ値に対して非常に敏感です。
・非線形関係のモデル化には適していません。
・線形回帰は、数値出力の予測に限定されます。
・説明変数の多重共線性や自己相関などの問題に対処する必要があります。
線形回帰の例
線形回帰のいくつかの具体的な手法とその説明は以下のようになります。
- 最小二乗法：目的変数と予測値の差の二乗和を最小化するようにパラメータを求める手法です。計算が簡単で、解が一意に定まりますが、外れ値や多重共線性に弱いです。
- リッジ回帰：最小二乗法にパラメータの大きさに対するペナルティ項を加えることで、過学習を防ぐ手法です。多重共線性に強く、汎化性能が高まりますが、パラメータの選択が難しいです。
- ラッソ回帰：最小二乗法にパラメータの絶対値に対するペナルティ項を加えることで、過学習を防ぐ手法です。不要な説明変数を自動的に除外する効果がありますが、解が一意に定まらない場合や計算時間が長くなる場合があります2。
- カーネル回帰：非線形関係をカーネル関数を用いて線形関係に写像することで、線形回帰を拡張した手法です。非線形関係も表現できるようになりますが、カーネル関数やハイパーパラメータの選択が難しいです。
最小二乗法
最小二乗法とは、測定で得られた数値の組を、適当なモデルから想定される関数を用いて近似するときに、想定する関数が測定値に対してよい近似となるように、残差平方和を最小とするような係数を決定する方法です。
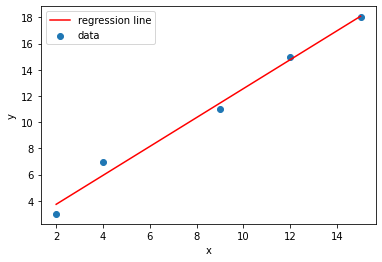
例として、データの組 (2,3), (4,7), (9,11), (12,15), (15,18) が与えられたときに、xとyの関係を表すもっともらしい直線 y=ax+b を求める場合、最小二乗法を適用すると、残差平方和 S を
S = (3 - (2a + b))^2 + (7 - (4a + b))^2 + (11 - (9a + b))^2 + (15 - (12a + b))^2 + (18 - (15a + b))^2と定義し、S が最小となるように a と b を求めます。S を a と b で偏微分して 0 とおくと、
a = 0.96, b = 0.92となり、もっともらしい直線は y=0.96x+0.92 となります。
最小二乗法の実装
最後にPythonによる最小二乗法の実装を紹介します。
# ライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
# データの定義
x = np.array([2, 4, 9, 12, 15])
y = np.array([3, 7, 11, 15, 18])
# 最小二乗法による直線の係数の計算
a, b = np.polyfit(x, y, 1) # 1次関数の係数を求める
print(f"a = {a}, b = {b}") # 係数の表示
# 直線の方程式
y_pred = a * x + b # 予測値
# グラフの描画
plt.scatter(x, y, label="data") # データの散布図
plt.plot(x, y_pred, color="red", label="regression line") # 回帰直線
plt.xlabel("x") # x軸のラベル
plt.ylabel("y") # y軸のラベル
plt.legend() # 凡例の表示
plt.show() # グラフの表示実行すると以下のようなグラフが出力されます。
G検定学習法
最後までご覧いただきありがとうございました。
当サイトではG検定に役立つ情報をまとめています。
ぜひご覧ください。
本サイトの活用方法
【G検定2024最新】試験当日も使える! 187項目の要点整理＆試験対策カンペ【新シラバス対応】
G検定の要点をシラバスから抜粋してまとめました。これから学習する方も、復習したい方にもお使いいただけます。試験当日用のG検定のカンニングペーパー参考としてもお役立てください。試験結果を保証するものではありませんので、試験 […]
G検定シラバス改訂の概要と変更のポイント
シラバス改訂の概要 一般社団法人日本ディープラーニング協会（JDLA）は、2024年11月実施の「G検定2024 #6」よりG検定（ジェネラリスト検定）のシラバスを改訂すると発表しました。 JDLAによると、今回の改訂で […]
【G検定2024まとめ】理解度確認問題集【直前対策】
問題 すべての問題の解答が終わると答えを見ることができます。 解説動画 関連記事【G検定2024最新】試験当日も使える! 187項目の要点整理＆試験対策カンペ【新シラバス対応】 2024年10月24日 G検定シ […]
【G検定まとめ2024】YouTube動画リスト（問題編）
講義編はこちら 関連記事【G検定2024最新】試験当日も使える! 187項目の要点整理＆試験対策カンペ【新シラバス対応】 2024年10月24日 G検定シラバス改訂の概要と変更のポイント 2024年6 […]
【G検定まとめ2024】YouTube動画リスト（講義編）
問題編はこちら 関連記事【G検定2024最新】試験当日も使える! 187項目の要点整理＆試験対策カンペ【新シラバス対応】 2024年10月24日 G検定シラバス改訂の概要と変更のポイント 2024年6 […]
【G検定まとめ2024】試験当日も使える! 要点整理＆試験対策カンペ【旧シラバス】
G検定の要点をシラバスから抜粋してまとめました。これから学習する方も、復習したい方にもお使いいただけます。試験当日用のG検定のカンニングペーパー参考としてもお役立てください。試験結果を保証するものではありませんので、試験 […]
参考書籍
①教科書として使用する書籍
体系的に知識を整理することができます。
まずは、この１冊を読んでG検定の学習を進めましょう。
検索機能が使用できるので、Kindle版が特におすすめです。
②問題集として使用する書籍
ある程度学習が進んだら、本番を意識して問題集に取り組みましょう。
本番の試験環境を意識して、このページ「要点整理＆当日用カンペ」を使用しながら解答してみましょう。
