【G検定まとめ】要点整理＆当日用カンペの項目別詳解ページです。

詳細な知識や実装は試験には必ずしも必須ではありませんが、試験対策として理解を深めたい方はぜひ最後までご覧ください。

G検定まとめはこちら

word2vecとは

単語をベクトルとして表現する手法で、2013年にgoogle 社のミコロフが枠組みを提案。分散表現を得る代表的な手法で、「単語の意味は、その周辺の単語によって決まる」という分布仮説をNNを用いて推論ベースで実現した手法であり、word2vecにはスキップグラムとCBOWという2つの手法がある。このようなモデルを「ベクトル空間モデル」や「単語埋め込みモデル」とも呼ぶ。単語の互いの意味の近さの計算や加減のような演算ができる。
word2vecの演算事例としてV（Prince） – V（Male） + V（Female） ≒ V（Princess）

word2vecと単語の分散表現

単語を固定長のベクトルで表現することを「単語の分散表現」と言います。

自然言語処理において機械学習を活用するためには、単語の持つ性質や意味を反映したベクトル表現を獲得することが重要となります。

単語をベクトルで表現することができれば、単語の意味を定量的に把握することができるため、様々な処理に応用することができます。

単語をベクトルで表現する方法として、one-hotベクトル、Word2Vec、fastTextといった手法が提案されてきました。

word2vecとは

Word2vecは、Googleの研究者であるトマス・ミコロフ氏が率いる研究チームによって2013年に公開されました。

2層のニューラルネットワークのみで構成されているということが特徴です。

構造がシンプルであるため、大規模なデータによる分散表現学習を現実的な計算量によって行えるようになり、分散表現での自然言語処理を飛躍的に進めることができました。

なお、「Word2vec」はスキップグラム法（skip-gram法）、CBOW(continuous bag-of-words)という2つの技術の集合です。

引用：https://arxiv.org/pdf/1301.3781.pdf

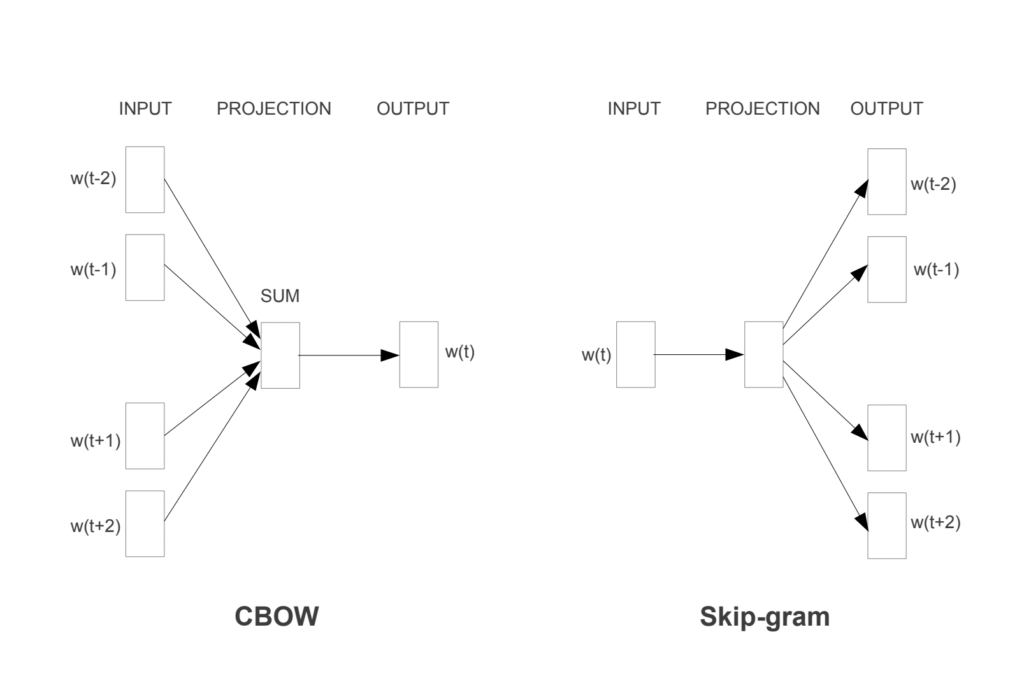
CBOW(continuous bag-of-words)

CBOWは、教師あり学習が用いられます。

周辺語を入力として付与し、その中心語の予測を出力する学習を行います。

どんな単語が現れる可能性があるかを理解することで、単語の意味関係を把握できるようになります。

skip-gram

スキップグラム法では、教師あり学習が用いられます。

CBOWとは反対に、中心語を入力として付与し、その周辺語の予測を出力する学習を行います。

単語の周りにどんな単語が現れる可能性があるかを理解することで、単語の意味関係を把握できるようになります。

word2vecの実装

学習済モデルを取得

まずは学習済モデルを用意します。

今回はこちらのモデルを使用させていただくことにします。

（出典：https://github.com/singletongue/WikiEntVec/releases/download/20190520/jawiki.word_vectors.200d.txt.）

早速、モデルをダウンロードします。

!wget https://github.com/singletongue/WikiEntVec/releases/download/20190520/jawiki.word_vectors.200d.txt.bz2
!bzip2 -d jawiki.word_vectors.200d.txt.bz2

ダウンロードしたモデルを読み込んでおきます。

gensimというライブラリを使用することで、Word2Vecを簡単に扱えるようになります。

# モデルを読み込む
from gensim import models
w2v_model =  models.KeyedVectors.load_word2vec_format('jawiki.word_vectors.200d.txt', binary=False)

以上で準備が完了しました。

Word2Vecによる単語ベクトル

単語ベクトル

まずは単語ベクトルを表示しています。

「男」という単語を例にします。

word = "男"

# Word2Vecで作成した単語ベクトルのshape
word_vec = w2v_model.wv.__getitem__(word)
print(word_vec.shape)

# Word2Vecで作成した単語ベクトル
print(word_vec)

実行すると、以下の通り出力されます。

(200,)
[ 0.015809   -0.3251379   0.05244135  0.06446267  0.05560444 -0.10130245
 -0.10580788 -0.14394113 -0.34319535 -0.10822236 -0.19849339 -0.26917374
  0.22541721 -0.07668435  0.48141098 -0.147957    0.43515927 -0.03782997
  0.2389156   0.01180182  0.1836466   0.16968328 -0.3920643   0.12813346
 -0.20881392  0.19826704  0.03449377 -0.04753834  0.2486179  -0.14926115
 -0.02117037 -0.3065304   0.3936741  -0.10212087 -0.04573085 -0.1337663
 -0.22365484  0.16874568  0.07610422  0.09013756 -0.29010847  0.18294546
 -0.5175267   0.07319862 -0.18262151 -0.05056991  0.1262936  -0.02267754
 -0.06510926 -0.01428416 -0.09494394  0.08261232  0.12032219 -0.01902988
  0.04504069 -0.13478482 -0.17759144 -0.14752197 -0.02539819  0.10928936
 -0.09864278  0.08571469  0.13544586  0.10696616 -0.03865746 -0.1618845
  0.04960717 -0.15753698  0.3267987   0.08656162 -0.01817252  0.13675034
 -0.3327987   0.2530842   0.12734842  0.06555606  0.160463    0.06241005
  0.23274134 -0.11655759  0.16264422  0.53337     0.15273613  0.36126742
  0.12710397 -0.0883073   0.16111715 -0.07801783 -0.05251171 -0.03803135
  0.36643884 -0.05368368 -0.08609699 -0.19484329  0.12814972  0.00330684
  0.07512157  0.15090348 -0.10693323  0.01813235 -0.2135235  -0.00780941
  0.05442232  0.24011889 -0.51129556 -0.638149    0.02244863 -0.22941312
 -0.23984718 -0.02993166 -0.05658468 -0.01124568  0.2406439   0.45328262
  0.19353937  0.30052927 -0.11227108 -0.0850492  -0.16737182 -0.33904943
  0.10570832 -0.09934106  0.03946824 -0.2834313  -0.04729119  0.2697491
  0.12789859 -0.17199114  0.41526002 -0.23899308 -0.45907646 -0.12020862
 -0.14896242 -0.04573169 -0.09786802 -0.1763842   0.12901594  0.02436519
  0.00428179 -0.36937413 -0.4695615  -0.22230782  0.2830068   0.2566159
  0.04325378  0.05985418  0.3014291   0.09938446  0.05811239  0.39835015
  0.164487   -0.14685854 -0.17889863 -0.02350353 -0.1620599  -0.3441901
  0.26197276 -0.294521   -0.05924391 -0.23041128  0.5574968   0.21000126
  0.10179501  0.01910508  0.3779993   0.01058383 -0.28017193  0.15513653
 -0.2171893  -0.27293232  0.1677527  -0.14999865  0.26054642  0.21831411
 -0.07688119  0.25424448  0.08557764 -0.08890117 -0.0325109  -0.18752629
  0.13194856  0.0568304   0.11748125  0.40530595 -0.3771344  -0.35576954
 -0.22595452 -0.15970773 -0.22661117  0.03037297  0.09092331 -0.01097557
  0.40739244 -0.01088747  0.28517485  0.10055861 -0.29882434  0.04821419
  0.15081635 -0.32244784]

類似度の高い単語を表示

単語をベクトル化することで、内積を計算できるようなります。

これにより、単語間の類似度を計算することが可能となりました。

まずは、「勉強」という単語の類似度が高い単語を表示する例を紹介します。

results = w2v_model.most_similar(positive=['勉強'])
for result in results:
    print(result)

実行すると、以下の通り出力されます。

('勉学', 0.8039138913154602)
('受験勉強', 0.7886025905609131)
('通い', 0.7718825340270996)
('学業', 0.7624354362487793)
('猛勉強', 0.7539629936218262)
('独学', 0.744247317314148)
('励ん', 0.7085117697715759)
('仕事', 0.7079863548278809)
('学び', 0.7079614400863647)
('教える', 0.7043171525001526)

コサイン類似度であるため、1に近いほど、より似ているということになります。

勉強に意味の近い単語が表示されていることがわかります。

復習単語の類似度が高い単語を表示する

復習単語の類似度が高い単語を表示する例を紹介します。

# 複数の単語で類似度の高いものを上から１０個表示する

results = w2v_model.most_similar(['北海道', 'ランチ'])
for result in results:
    print(result)

実行すると、以下の通り出力されます。

('グルメフェスタ', 0.6769476532936096)
('ELLCUBE', 0.6654763221740723)
('食材王国', 0.6653890609741211)
('新富良野プリンスホテル', 0.661788284778595)
('ステラプレイス', 0.6588473320007324)
('サッポロファクトリー', 0.6588059067726135)
('YAKINIKU', 0.657869815826416)
('FMわっぴ', 0.6575604677200317)
('空弁', 0.6536294221878052)
('函館', 0.6521193981170654)

単語の意味を足し引きして類似度が高い単語を表示する

単語の意味を足し引きして、類似度が高い単語を表示する例を紹介します。

# 単語の意味を足し引きして、類似度の高いものを上から１０個表示する
results = w2v_model.most_similar(positive=['エンジニア'], negative=['プログラミング'])
for result in results:
    print(result)

実行すると、以下の通り出力されます。

('チーフ', 0.418521523475647)
('技師', 0.3822118043899536)
('マネージングディレクター', 0.37540167570114136)
('責任者', 0.37215274572372437)
('録音技師', 0.3719862699508667)
('チーフエアロダイナミシスト', 0.3683624267578125)
('フィオリオ', 0.3636731207370758)
('重役', 0.3555722236633301)
('マネージング・ディレクター', 0.35550376772880554)
('働い', 0.3503777086734772)

２つの単語の類似度を算出する

２つの単語の類似度を表示する例を紹介します。

# ２つの単語の類似度を算出する
results = w2v_model.similarity('小学校', '中学校')
print(results)

実行すると、以下の通り出力されます。

0.90959257

2つの単語の意味が似ていることを定量的に確認することができました。

G検定学習法

最後までご覧いただきありがとうございました。

当サイトではG検定に役立つ情報をまとめています。

ぜひご覧ください。

本サイトの活用方法

【G検定2024最新】試験当日も使える! 187項目の要点整理＆試験対策カンペ【新シラバス対応】
2024年10月24日

G検定の要点をシラバスから抜粋してまとめました。これから学習する方も、復習したい方にもお使いいただけます。試験当日用のG検定のカンニングペーパー参考としてもお役立てください。試験結果を保証するものではありませんので、試験 […]

G検定シラバス改訂の概要と変更のポイント
2024年6月23日

シラバス改訂の概要 一般社団法人日本ディープラーニング協会（JDLA）は、2024年11月実施の「G検定2024 #6」よりG検定（ジェネラリスト検定）のシラバスを改訂すると発表しました。 JDLAによると、今回の改訂で […]

【G検定2024まとめ】理解度確認問題集【直前対策】
2024年5月28日

問題 すべての問題の解答が終わると答えを見ることができます。 解説動画 関連記事【G検定2024最新】試験当日も使える! 187項目の要点整理＆試験対策カンペ【新シラバス対応】 2024年10月24日 G検定シ […]

【G検定まとめ2024】YouTube動画リスト（問題編）
2024年5月4日

講義編はこちら 関連記事【G検定2024最新】試験当日も使える! 187項目の要点整理＆試験対策カンペ【新シラバス対応】 2024年10月24日 G検定シラバス改訂の概要と変更のポイント 2024年6 […]

【G検定まとめ2024】YouTube動画リスト（講義編）
2024年1月24日

問題編はこちら 関連記事【G検定2024最新】試験当日も使える! 187項目の要点整理＆試験対策カンペ【新シラバス対応】 2024年10月24日 G検定シラバス改訂の概要と変更のポイント 2024年6 […]

【G検定まとめ2024】試験当日も使える! 要点整理＆試験対策カンペ【旧シラバス】
2024年1月1日

G検定の要点をシラバスから抜粋してまとめました。これから学習する方も、復習したい方にもお使いいただけます。試験当日用のG検定のカンニングペーパー参考としてもお役立てください。試験結果を保証するものではありませんので、試験 […]

参考書籍

①教科書として使用する書籍

体系的に知識を整理することができます。

まずは、この１冊を読んでG検定の学習を進めましょう。

検索機能が使用できるので、Kindle版が特におすすめです。

②問題集として使用する書籍

ある程度学習が進んだら、本番を意識して問題集に取り組みましょう。

本番の試験環境を意識して、このページ「要点整理＆当日用カンペ」を使用しながら解答してみましょう。

カテゴリー
G検定、資格
タグ
前の記事
【G検定】分散表現
2023年1月2日
次の記事
【G検定】人工知能とは何か
2023年1月4日