このシリーズではE資格対策として、書籍「ゼロから作るDeep Learning」を参考に学習に役立つ情報をまとめています。
<参考書籍>
画像の分析手法
画像認識の分野では、これまでの特徴量を用いた手法とニューラルネットワークという2つの主要なアプローチがあります。
特徴量を使った画像認識
これまでの画像認識の手法では、画像から特徴量(特徴)を抽出し、それらを基に画像のクラス(例:犬、猫など)を判断します。特徴量とは、画像の形状、色、テクスチャなどの情報です。特徴量を抽出する方法として、SIFTやHOGなどのアルゴリズムがよく使われました。抽出された特徴量は、分類器(例:SVM)に入力され、最終的に画像がどのクラスに属するかを判断します。
ニューラルネットワーク
ニューラルネットワークは人間の脳の仕組みにヒントを得たアルゴリズムで、画像認識に非常に効果的です。ニューラルネットワークは、多数の層(レイヤー)で構成されており、それぞれの層が特定の機能を担当しています。入力層は画像データを受け取り、出力層は最終的な分類結果を出力します。中間層(隠れ層)では、画像の特徴量が自動的に学習されます。
特徴量を使った画像認識とニューラルネットワークの比較
上記手法について比較結果をまとめと以下のようになります。
| 特徴量抽出 | 特徴量を使った手法では、人間が考えた特徴量抽出のアルゴリズムを使いますが、ニューラルネットワークは自動的に特徴量を学習します。 |
| 柔軟性 | ニューラルネットワークは、複雑なパターンや階層的な構造を表現する能力があり、特徴量を使った手法よりも柔軟性があります。 |
| 学習能力 | ニューラルネットワークは、大量のデータや高次元のデータでも効果的に学習できるため、より複雑な問題に対処できます。ルネットワークは、複雑なパターンや階層的な構造を表現する能力があり、特徴量を使った手法よりも柔軟性があります。 |
ニューラルネットワークのメリット
ニューラルネットワークのメリットをまとめと以下のようになります。
| 自動特徴学習 | ニューラルネットワークは、データから自動的に有用な特徴量を学習するため、人間が手作業で特徴量を設計する必要がありません。 |
| 高い性能 | 大量のデータと深い層を持つニューラルネットワークは、特徴量ベースの手法よりも高い認識性能を達成できます。特に、ディープラーニング(深層学習)と呼ばれる深いニューラルネットワークは、画像認識や音声認識などの分野で驚異的な成果を収めています。 |
| 汎用性 | ニューラルネットワークは、画像認識だけでなく、自然言語処理や強化学習など、さまざまなタスクにも適用可能です。これは、ニューラルネットワークが自動的にデータから特徴量を学習するため、多様な問題に対応できるからです。 |
訓練データとテストデータ
訓練データとテストデータは、機械学習やディープラーニングのタスクを行う際に使用するデータの2つの主要な種類です。これらは、モデルの学習と評価にそれぞれ用いられます。
| 訓練データ (Training data) | 訓練データは、ニューラルネットワークや機械学習アルゴリズムが学習するために使われるデータです。訓練データを使用して、モデルのパラメータ(重みとバイアス)を最適化し、データからパターンや特徴量を抽出することが目的です。訓練データは通常、全体のデータセットの大部分(例えば、70%~80%)を占めます。 |
| テストデータ (Test data) | テストデータは、学習が完了したモデルの性能を評価するために使用されるデータです。テストデータは、学習プロセスで使用されないデータの一部で、モデルが未知のデータに対してどれくらい正確に予測できるかを測定する目的で使われます。一般的に、全体のデータセットのうち20%~30%がテストデータとして利用されます。 |
訓練データとテストデータに分割することのメリット
データセット全体を訓練データとテストデータに分割することにより、以下の利点があります。
| 過学習(オーバーフィッティング)の検出 | モデルが訓練データに対しては高い性能を示すものの、未知のデータに対しては低い性能を示す場合、過学習が発生している可能性があります。テストデータを使ってモデルの性能を評価することで、過学習の兆候を検出できます。 |
| モデルの汎化性能の評価 | テストデータを用いてモデルの評価を行うことで、未知のデータに対するモデルの予測性能(汎化性能)を測定することができます。高い汎化性能を持つモデルは、新しいデータに対しても適切な予測を行うことが期待できます。 |
| モデルの比較 | 複数のモデルやアルゴリズムを比較する際、テストデータを使ってそれぞれのモデルの性能を評価できます。これにより、最も適切なモデルを選択することが可能になります。 |
注意点として、テストデータはモデルの評価にのみ使用されるべきであり、学習プロセスには使用されないことが重要です。テストデータを学習に使用してしまうと、モデルはそのデータに過剰に適合し、実際の未知データに対する性能が低下する可能性があります。また、訓練データとテストデータ以外に、検証データ(Validation data)という種類のデータも存在します。検証データは、訓練データの一部を分割して作成され、モデルのハイパーパラメータ(学習率や層の数など)の調整や、学習の進行状況を監視するために使用されます。検証データを使ってモデルの性能を定期的に評価し、過学習が発生していないかを確認することができます。
データの分割
通常、データセットは訓練データ、検証データ、テストデータの3つに分割されます。例えば、データセット全体を60%の訓練データ、20%の検証データ、20%のテストデータに分割することが一般的です。この方法で、モデルの学習、ハイパーパラメータの調整、最終的な性能評価が適切に行われることが保証されます。
データを適切に分割することで、以下の目的が達成できます。
| モデルの適切な評価 | モデルが未知のデータに対してどれくらい効果的に機能するかを正確に評価することができます。これにより、実際にデプロイした際に期待通りの性能を発揮するモデルを選択することができます。 |
| ハイパーパラメータの最適化 | 検証データを用いてハイパーパラメータを調整することで、モデルの性能を最大限に引き出すことができます。検証データを使用していくつかのハイパーパラメータの候補を試し、最も良い結果を得られる設定を採用することができます。 |
| 過学習の防止 | 学習プロセス中に検証データでの性能を監視することで、過学習が発生しているかどうかを把握し、適切な時点で学習を停止させることができます。これは、早期停止(Early stopping)と呼ばれるテクニックで、モデルが訓練データに過剰に適合するのを防ぎます。 |
データセットを訓練データ、検証データ、テストデータに分割する際には、データのランダム性を保つことが重要です。データをランダムに分割することで、分布の偏りや特定のパターンが学習に影響を与えることを避けられます。また、分類問題の場合、データセット内の各クラスのバランスを維持する層化抽出法(Stratified sampling)を使用すると、より効果的なデータ分割が可能です。
損失関数はなぜ必要なのか
損失関数(Loss function)は、機械学習やディープラーニングのモデルが学習する際に必要な要素です。損失関数は、モデルの予測結果と実際の目標値(正解ラベル)との差を数値化し、その差がどれだけ大きいかを評価する指標です。損失関数が必要な理由は以下の通りです。
- モデルのパフォーマンスの評価: 損失関数の値が小さいほど、モデルの予測が正解ラベルに近いことを意味します。損失関数を使って、モデルの性能を定量的に評価し、改善の必要性や方向性を判断することができます。
- パラメータの最適化: 損失関数を最小化するようにモデルのパラメータ(重みとバイアス)を更新することで、学習が進みます。損失関数は、パラメータの調整において目標となる指標であり、最適化アルゴリズム(例:確率的勾配降下法やAdam)が損失関数の勾配情報を利用して、パラメータを更新します。これにより、モデルは予測性能が向上し、データからのパターンや特徴を学習することができます。
- 適切なモデルの選択: 様々なモデルやアルゴリズムが存在しますが、それぞれのモデルに対して損失関数を計算することで、どのモデルが最も良い性能を持っているかを比較することができます。損失関数の値が最も小さいモデルが、最も適切なモデルとして選択されることが一般的です。
- 学習の進行状況の監視: 損失関数の値は、学習プロセス全体を通して監視されます。学習が進むにつれて、損失関数の値は通常減少し、モデルの性能が向上していることを示します。もし損失関数の値が減少しない場合、学習が適切に進行していない可能性があり、モデルのアーキテクチャや学習率などのハイパーパラメータを見直す必要があります。
損失関数は、学習タスクの目的に応じて選択されます。例えば、回帰問題の場合、平均二乗誤差(Mean Squared Error, MSE)がよく使用される損失関数です。一方、分類問題では、クロスエントロピー損失(Cross-Entropy Loss)が一般的に用いられます。
2乗和誤差
2乗和誤差(Squared Sum Error, SSE)は、回帰問題において使用される損失関数の一つです。2乗和誤差は、モデルの予測値と実際の目標値(正解ラベル)との差を二乗し、それらの和を計算します。2乗和誤差の数式は以下のように表されます。
ここで、y は実際の目標値、ŷ はモデルによる予測値です。Σは、すべてのデータポイントに対して和を取ることを示しています。
2乗和誤差は、以下のような特徴があります。
- 値が非負: 差の2乗を計算しているため、2乗和誤差の値は常に非負です。これにより、損失関数の値が0に近いほど予測が正確であることを意味します。
- 外れ値に敏感: 二乗を取っているため、外れ値(大きな誤差を持つデータポイント)はより大きなペナルティを受けます。このため、モデルは外れ値に対して強く適合しようとします。
ただし、2乗和誤差は単純に和を取っているため、データ数の影響を受けやすいです。そのため、データ数によらない評価指標として平均二乗誤差(Mean Squared Error, MSE)がよく使われます。MSEは、2乗和誤差をデータ数で割った値で、以下のように表されます。
MSEの実装(計算過程あり)
以下のMNISTの推論結果を例に、2乗和誤差を実装してみましょう。
この例では、ニューラルネットによる推論結果と実際の正解データの例となります。
# ニューラルネットワークの出力
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
# 正解データ
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])この例をもとに、まずは計算過程がわかるように出力してみます。
import numpy as np
# ニューラルネットワークの出力
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
# 正解データ
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])
# 2乗和誤差を計算する関数
def mean_squared_error(y, t):
# 出力と教師データの差分を計算
diff = y - t
print("差分:", diff)
# 差分を二乗
squared_diff = diff ** 2
print("二乗した差分:", squared_diff)
# 二乗した差分の合計を求め、データ数で割って平均を計算
mse = np.sum(squared_diff) / len(y)
print("二乗和誤差の平均:", mse)
return mse
# 2乗和誤差の計算
mse = mean_squared_error(y, t)実行結果:
差分: [ 0.1 0.05 -0.4 0. 0.05 0.1 0. 0.1 0. 0. ]
二乗した差分: [0.01 0.0025 0.16 0. 0.0025 0.01 0. 0.01 0. 0. ]
二乗和誤差の平均: 0.019500000000000007それぞれの差分を計算し、その2乗の値の総和をとって、最後にデータ数で割っています。
MSEの実装
途中経過を省略してまとめると以下のようになります。
import numpy as np
# ニューラルネットワークの出力を作成
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
# 教師データを作成
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])
# 2乗和誤差を計算する関数
def mean_squared_error(y, t):
# 出力と教師データの差分を計算
diff = y - t
# 差分を二乗
squared_diff = diff ** 2
# 二乗した差分の合計を求め、データ数で割って平均を計算
mse = np.sum(squared_diff) / len(y)
return mse
# 2乗和誤差の計算
mse = mean_squared_error(y, t)
print("Mean Squared Error:", mse)実行結果:
二乗和誤差の平均: 0.019500000000000007交差エントロピー誤差
交差エントロピー誤差はモデルの予測確率分布と正解の確率分布との間の類似度を測るために使用されます。具体的には、交差エントロピー誤差は予測確率分布が正解の確率分布にどれだけ近いかを評価し、その距離を最小化するようにモデルを最適化します。
交差エントロピー誤差は以下の式で表されます:
ここで、p(x) は正解の確率分布を、q(x) はモデルによる予測確率分布を表します。Σは、全てのクラスにわたる和を取ることを示しています。この式により、予測が正解と一致するときに損失が小さくなり、一致しないときに損失が大きくなるため、モデルは損失を最小化するように学習します。確率的な予測と実際のラベルとの間の不一致を効果的に評価できるため、多クラス分類問題やニューラルネットワークの学習に広く利用されています。
交差エントロピー誤差のグラフ
2つの確率分布がどれだけ近いかを視覚的に理解するために、2つのクラスがある場合の交差エントロピー誤差をグラフで表すことができます。以下のコードは、バイナリ分類問題(クラスが2つだけ)に対して、交差エントロピー誤差のグラフを描画する例です。
import numpy as np
import matplotlib.pyplot as plt
# 真の確率分布 (バイナリ分類の場合)
y_true = np.array([1, 0])
# 交差エントロピー誤差関数の定義
def binary_cross_entropy_error(y_true, y_pred):
return -np.sum(y_true * np.log(y_pred + 1e-7))
# 予測確率分布の範囲 (0.01 から 0.99 まで 0.01 刻み)
predictions = np.arange(0.01, 1, 0.01)
# 交差エントロピー誤差を計算
errors = [binary_cross_entropy_error(y_true, np.array([pred, 1 - pred])) for pred in predictions]
# グラフの表示
plt.plot(predictions, errors)
plt.xlabel('Prediction for Class 1')
plt.ylabel('Cross Entropy Error')
plt.title('Cross Entropy Error for Binary Classification')
plt.grid()
plt.show()実行結果:
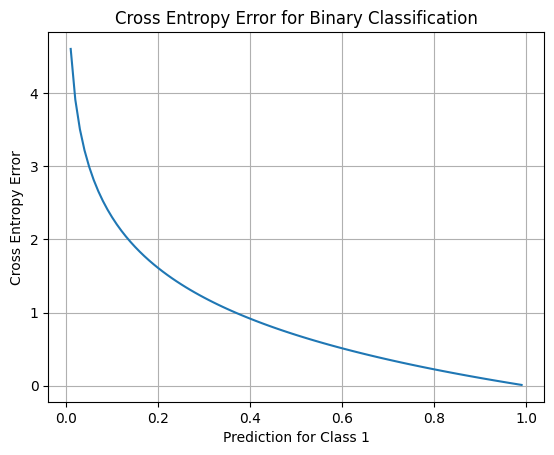
この結果は、バイナリ分類問題(クラスが2つだけ)に対して交差エントロピー誤差のグラフを表示しています。グラフは、予測確率が正解確率分布(クラス1が正解)に近づくと交差エントロピー誤差が小さくなり、遠ざかると大きくなることを示しています。
交差エントロピー誤差の実装(途中経過あり)
以下のMNISTの推論結果を例に、交差エントロピー誤差を実装してみましょう。
この例では、ニューラルネットによる推論結果と実際の正解データの例となります。
# ニューラルネットワークの出力
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
# 正解データ
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])この例をもとに、まずは計算過程がわかるように出力してみます。
import numpy as np
def cross_entropy_error(y, t):
delta = 1e-7 # ゼロ除算を防ぐための微小な値
return -np.sum(t * np.log(y + delta))
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])
# ステップ1: t * np.log(y + delta) を計算
step1 = t * np.log(y + 1e-7)
print("Step 1: t * np.log(y + delta):\n", step1)
# ステップ2: ステップ1の結果を合計する
step2 = -np.sum(step1)
print("Step 2: -np.sum(step1):\n", step2)
# エントロピー交差誤差を計算
loss = cross_entropy_error(y, t)
print("Final Loss:\n", loss)実行結果:
Step 1: t * np.log(y + delta):
[-0. -0. -0.51082546 -0. -0. -0. -0. -0. -0. -0.]
Step 2: -np.sum(step1):
0.510825457099338
Final Loss:
0.510825457099338エントロピー交差誤差の計算過程を2つのステップに分けて表示しています。
- ステップ1では、
t * np.log(y + delta)を計算しています。このステップでは、教師データ(t)とニューラルネットワークの出力(y)の各要素ごとに、t_i * log(y_i)を計算します。 - ステップ2では、ステップ1で計算された値の合計を計算します。この合計がエントロピー交差誤差です。
最後に、得られたエントロピー交差誤差の値(loss)を表示しています。
交差エントロピー誤差の実装
途中経過を省略してまとめると以下のようになります。
import numpy as np
def cross_entropy_error(y, t):
delta = 1e-7 # ゼロ除算を防ぐための微小な値
return -np.sum(t * np.log(y + delta))
y = np.array([0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0])
t = np.array([0, 0, 1, 0, 0, 0, 0, 0, 0, 0])
# エントロピー交差誤差を計算
loss = cross_entropy_error(y, t)
print(loss)実行結果:
0.510825457099338エントロピー交差誤差が小さいほど、ニューラルネットワークの出力が教師データに近いことを意味します。逆にエントロピー交差誤差が大きいほど、ニューラルネットワークの出力が教師データから離れていることを意味します。
まとめ
最後までご覧いただきありがとうございました。
