【E資格】第9回:勾配と勾配法【ゼロから作るDeep Learning】

このシリーズではE資格対策として、書籍「ゼロから作るDeep Learning」を参考に学習に役立つ情報をまとめています。

<参考書籍>

勾配

ある関数のある点での勾配は、その点における接線の傾きに相当します。勾配は、関数の変化の速さや方向を理解するのに役立ちます。

数学的には、微分可能な関数f(x)のある点x=aでの勾配は、その点での導関数f'(a)の値として定義されます。導関数f'(x)は、関数の変化の割合を表す新しい関数で、xの微小な変化に対するf(x)の変化を記述します。

たとえば、位置と時間の関数f(t)が与えられた場合、その勾配は速度を意味します。この場合、導関数f'(t)は速度の関数であり、ある時刻tでの勾配はその時刻での速度を表します。

勾配は、最適化問題や機械学習、物理学などのさまざまな分野で重要な役割を果たします。例えば、勾配降下法は機械学習アルゴリズムで最適なパラメータを見つける際に使用され、物理学では勾配は物体の運動や力の働きを解析する際に利用されます。

勾配の実装

以下に、例として一次関数（y = 2x）の勾配を求めるコードを示します。

def function(x):
    return 2 * x

def numerical_gradient(f, x, h=1e-5):
    return (f(x + h) - f(x - h)) / (2 * h)

x = 3
gradient = numerical_gradient(function, x)
print(f"勾配: {gradient}")

実行結果:

勾配: 2.0000000000131024

勾配の可視化

2変数関数（f(x0, x1) = x0^2 + x1^2）の勾配を計算し、それを2次元平面上にベクトル場として可視化しています。

import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D

# 数値微分を用いて、1次元入力に対する勾配を計算する関数
def _numerical_gradient_no_batch(f, x):
    h = 1e-4  # 0.0001
    grad = np.zeros_like(x)
    
    # 各次元に対して勾配を計算
    for idx in range(x.size):
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x)  # f(x+h)
        
        x[idx] = tmp_val - h 
        fxh2 = f(x)  # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val  # 値を元に戻す
        
    return grad

# 数値微分を用いて、1次元または2次元入力に対する勾配を計算する関数
def numerical_gradient(f, X):
    if X.ndim == 1:
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X)
        
        # 各行に対して勾配を計算
        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_no_batch(f, x)
        
        return grad

# 2変数関数f(x0, x1) = x0^2 + x1^2を定義
def function_2(x):
    if x.ndim == 1:
        return np.sum(x**2)
    else:
        return np.sum(x**2, axis=1)

# この関数は使用されていませんが、接線の方程式を返す機能を持っています
def tangent_line(f, x):
    d = numerical_gradient(f, x)
    print(d)
    y = f(x) - d*x
    return lambda t: d*t + y

# メイン部分
if __name__ == '__main__':
    # 点の格子を生成するための範囲を定義
    x0 = np.arange(-2, 2.5, 0.25)
    x1 = np.arange(-2, 2.5, 0.25)
    # 格子を作成
    X, Y = np.meshgrid(x0, x1)
    
    # 格子上の点を平坦化
    X = X.flatten()
    Y = Y.flatten()

    # 各点に対して勾配を計算
    grad = numerical_gradient(function_2, np.array([X, Y]).T).T

    # 勾配ベクトルをプロット
    plt.figure()
    plt.quiver(X, Y, -grad[0], -grad[1],  angles="xy",color="#666666")
    plt.xlim([-2, 2])
    plt.ylim([-2, 2])
    plt.xlabel('x0')
    plt.ylabel('x1')
    plt.grid()
    plt.draw()
    # 結果を表示
    plt.show()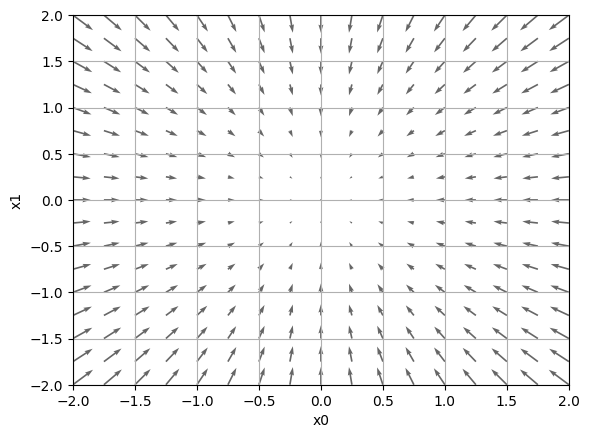

関数f(x0, x1) = x0^2 + x1^2は原点に極小値（最小値）を持つため、勾配ベクトルは、各点から原点へ向かっていることが視覚的に確認できます。この可視化は、最適化アルゴリズム（例えば勾配降下法）の挙動を理解するのに役立ちます。勾配降下法では、勾配ベクトルの逆方向に徐々にパラメータを更新していくことで、最小値に収束させようとします。この例では、最小値は原点にあるため、各点での勾配ベクトルは原点へ向かっています。

勾配法

勾配法は、最適化問題を解くための一般的な手法で、主にニューラルネットワークや深層学習の訓練に使用されます。これは、目的関数（コスト関数や損失関数とも呼ばれる）を最小化するようなモデルのパラメータを見つけることを目的としています。勾配法では、まずモデルのパラメータをランダムな値や特定の方法で初期化し、次に目的関数に対する各パラメータの勾配を計算します。勾配は、目的関数が最も急速に増加する方向を示しています。

計算された勾配を用いて、パラメータを更新します。一般的には、学習率というハイパーパラメータを用いて、勾配の方向に対してパラメータを更新することで、目的関数の値を徐々に減らしていきます。勾配の大きさがある閾値以下になるか、最大のイテレーション回数に達するまで、勾配の計算とパラメータの更新を繰り返します。

勾配法にはいくつかのバリエーションがあります。基本的な勾配降下法では、全てのデータポイントを用いて勾配を計算し、パラメータを更新します。確率的勾配降下法では、各イテレーションでランダムに選択された1つのデータポイントを用いて勾配を計算し、パラメータを更新します。これにより、計算負荷が軽減され、局所最適解に陥るリスクが低減されます。ミニバッチ勾配降下法では、各イテレーションでランダムに選択された一部のデータポイント（ミニバッチ）を用いて勾配を計算し、パラメータを更新します。これは、計算効率と収束速度のバランスを取るための方法です。

機械学習と勾配法

機械学習モデルの訓練では、目的関数（またはコスト関数、損失関数）を最小化するようなモデルのパラメータを見つけることが目的です。勾配法は、目的関数が最も急速に増加する方向（勾配）を利用して、パラメータを更新することで、この最小化問題を解決します。勾配法が有効な理由の一つは、勾配が目的関数の局所的な特性を反映していることです。これにより、各更新ステップで目的関数の値を効果的に減らすことができます。また、勾配法はイテレーションベースのアプローチであるため、大規模なデータセットや複雑なモデルにも適用可能です。イテレーションを繰り返すことで、徐々に最適なパラメータに近づくことができます。さらに、勾配法は多様な最適化アルゴリズムを利用できる点でも有効です。例えば、確率的勾配降下法（SGD）やミニバッチ勾配降下法は、計算負荷を軽減し、局所最適解への影響を抑制します。他にも、モーメンタムやアダム（Adam）といった最適化アルゴリズムは、過去の勾配情報を利用して、パラメータ更新の効率を向上させることができます。

鞍点

鞍点とは、最適化問題において特定の点が、ある次元では局所的な最小値となる一方で、他の次元では局所的な最大値となる現象です。これは、多次元空間において、目的関数（コスト関数や損失関数とも呼ばれる）の形状が鞍のようになるため、鞍点と呼ばれます。

鞍点は、勾配法を用いた最適化アルゴリズムにおいて問題となることがあります。勾配法では、目的関数の勾配を計算し、その勾配がゼロに近い値になるまでパラメータを更新していくことで、最適なパラメータを見つけようとします。しかし、鞍点では、勾配がゼロになるため、最適化アルゴリズムが停滞し、最適な解に到達できなくなることがあります。

特に、ニューラルネットワークや深層学習においては、高次元のパラメータ空間を探索するため、鞍点に陥る確率が高くなります。この問題に対処するため、様々な最適化アルゴリズムが提案されています。例えば、確率的勾配降下法（SGD）は、各イテレーションでランダムに選択されたデータポイントを用いて勾配を計算するため、局所最適解や鞍点から抜け出す可能性が高まります。また、モーメンタムやアダム（Adam）などの最適化アルゴリズムは、過去の勾配の情報を利用して、鞍点や局所最適解を乗り越える能力を向上させています。

鞍点を持つ関数（x^2 - y^2）を実装すると以下のようになります。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def saddle_point_function(x, y):
    return x ** 2 - y ** 2

# グリッドの作成
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)

# 鞍点関数の計算
z = saddle_point_function(x, y)

# 3Dグラフの描画
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d")
ax.plot_surface(x, y, z, cmap="viridis", alpha=0.8)

# グラフの設定
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
ax.set_title("Saddle Point Function")

# グラフの表示
plt.show()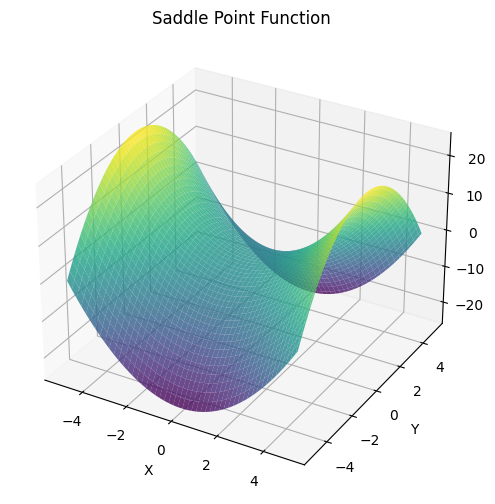

プラトー

プラトーは、最適化問題の解探索中に、目的関数（またはコスト関数、損失関数）の値がほとんど変化せず、平坦な領域になる現象を指します。プラトーが発生すると、最適化アルゴリズムが停滞し、訓練プロセスが遅くなることがあります。これは、勾配が非常に小さいため、パラメータの更新がほとんど行われないからです。プラトーは、機械学習のモデル、特に深層学習モデルの訓練においてよく遭遇する問題です。プラトーに対処するために、いくつかの方法が提案されています。まず、学習率の調整があります。固定の学習率ではなく、訓練の進行に応じて学習率を変化させることで、プラトーを抜け出す可能性が高まります。

また、最適化アルゴリズム自体を改善することも有効です。例えば、モーメンタムを用いることで、過去の勾配の情報を利用し、パラメータの更新方向をより滑らかにし、プラトーをより効率的に抜け出すことができます。その他の最適化アルゴリズム、例えばアダム（Adam）やRMSpropなども、プラトーへの対処を改善する目的で開発されています。バッチ正規化（Batch Normalization）や重みの初期化戦略の選択など、モデルのアーキテクチャを工夫することも、プラトーの問題を緩和する効果があります。これらの方法を適切に組み合わせることで、プラトーによる訓練の遅延を最小限に抑えることができます。

学習率

学習率は、最適化アルゴリズムにおいてパラメータを更新する際のステップサイズを決定する重要なハイパーパラメータです。勾配法を用いた最適化アルゴリズムでは、目的関数（またはコスト関数、損失関数）の勾配に基づいてモデルのパラメータを更新しますが、その際にどれだけパラメータを変更するかを決める役割が学習率にあります。

適切な学習率を選択することは、機械学習モデルの訓練において非常に重要です。学習率が大きすぎる場合、パラメータが大きく変動しすぎて、最適解を飛び越えることがあります。これは、モデルが収束せず、訓練が不安定になる原因となります。一方で、学習率が小さすぎる場合、パラメータの更新が非常に遅くなり、モデルの訓練に多くの時間がかかることになります。さらに、学習率が小さすぎると、モデルが局所最適解に陥りやすくなることがあります。

学習率の調整には、様々な戦略があります。固定学習率を使用するのではなく、訓練の進行に応じて学習率を動的に変更するスケジューリング手法が一般的です。例えば、学習率を段階的に減少させるステップ減衰や、指数関数的に減少させる指数減衰などがあります。また、アダプティブな学習率を持つ最適化アルゴリズム（例：アダム、RMSprop）も存在し、これらは各パラメータに対して個別に学習率を調整することができます。

勾配降下法を実装

勾配降下法を実装して、二次元平面上での収束過程を可視化します。

import numpy as np
import matplotlib.pylab as plt

# 数値微分を計算する関数
def numerical_gradient(f, X):
    if X.ndim == 1:
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X)
        
        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_no_batch(f, x)
        
        return grad

# 勾配降下法を実装する関数
def gradient_descent(f, init_x, lr=0.01, step_num=100):
    x = init_x
    x_history = []

    for i in range(step_num):
        x_history.append( x.copy() )

        grad = numerical_gradient(f, x)
        x -= lr * grad

    return x, np.array(x_history)

# 最適化対象の関数（二次元平面上の放物面）
def function_2(x):
    return x[0]**2 + x[1]**2

# 初期値を設定
init_x = np.array([-3.0, 4.0])    

# 学習率とステップ数を設定
lr = 0.1
step_num = 20
x, x_history = gradient_descent(function_2, init_x, lr=lr, step_num=step_num)

# グラフに結果をプロット
plt.plot( [-5, 5], [0,0], '--b')
plt.plot( [0,0], [-5, 5], '--b')
plt.plot(x_history[:,0], x_history[:,1], 'o')

# グラフの表示範囲を設定
plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("X0")
plt.ylabel("X1")

# グラフを表示
plt.show()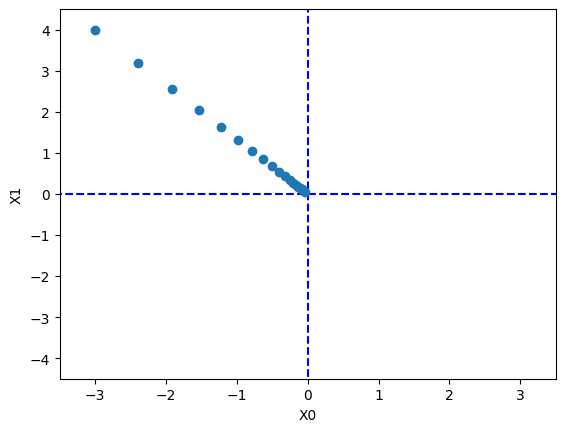

まとめ

最後までご覧いただきありがとうございました。