このシリーズではE資格対策として、書籍「ゼロから作るDeep Learning」を参考に学習に役立つ情報をまとめています。
<参考書籍>
更新手法の比較
異なる最適化アルゴリズム(SGD, Momentum, AdaGrad, Adam)を使用してパラメータを更新する様子を比較します。それぞれの最適化アルゴリズムを使用してパラメータの更新を30回行い、その過程をプロットしています。また、関数fの等高線も描画して、パラメータの更新がどのように関数の形状に従って行われるかを視覚的に理解することができます。
# 必要なライブラリとモジュールをインポート
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
# 勾配降下法(Stochastic Gradient Descent: SGD)のクラスを定義
class SGD:
def __init__(self, lr=0.01): # 初期化メソッドで学習率を設定
self.lr = lr
def update(self, params, grads): # パラメータを更新するメソッド
for key in params.keys():
params[key] -= self.lr * grads[key] # 勾配に学習率を掛けてパラメータを更新
# モメンタム法(Momentum)のクラスを定義
class Momentum:
def __init__(self, lr=0.01, momentum=0.9): # 初期化メソッドで学習率とモメンタムを設定
self.lr = lr
self.momentum = momentum
self.v = None # 速度を表す変数を初期化
def update(self, params, grads): # パラメータを更新するメソッド
if self.v is None:
self.v = {}
for key, val in params.items(): # 初回時に速度をパラメータと同じ形状で初期化
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] # 速度を更新
params[key] += self.v[key] # パラメータを更新
# AdaGrad法のクラスを定義
class AdaGrad:
def __init__(self, lr=0.01): # 初期化メソッドで学習率を設定
self.lr = lr
self.h = None # 勾配の二乗和を保持する変数を初期化
def update(self, params, grads): # パラメータを更新するメソッド
if self.h is None:
self.h = {}
for key, val in params.items(): # 初回時にhをパラメータと同じ形状で初期化
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key] # 勾配の二乗和を更新
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7) # パラメータを更新
# Adam法のクラスを定義
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999): # 初期化メソッドで学習率とbeta1,beta2を設定
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None # 1次モーメント推定値を保持する変数を初期化
self.v = None # 2次モーメント推定値を保持する変数を初期化
def update(self, params, grads): # パラメータを更新するメソッド
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items(): # 初回時にmとvをパラメータと同じ形状で初期化
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key]) # mを更新
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key]) # vを更新
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7) # パラメータを更新
# 関数fとその微分dfを定義
def f(x, y):
return x**2 / 20.0 + y**2
def df(x, y):
return x / 10.0, 2.0*y
# 初期位置とパラメータ、勾配の初期化
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
# 最適化手法の辞書を定義
optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)
idx = 1
# 各最適化手法について
for key in optimizers:
optimizer = optimizers[key]
x_history = []
y_history = []
params['x'], params['y'] = init_pos[0], init_pos[1]
# 30回のパラメータ更新を実行
for i in range(30):
x_history.append(params['x'])
y_history.append(params['y'])
grads['x'], grads['y'] = df(params['x'], params['y'])
optimizer.update(params, grads) # パラメータを更新
# 関数fの値を格子点上で計算
x = np.arange(-10, 10, 0.01)
y = np.arange(-5, 5, 0.01)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
# 等高線描画のためのマスクを作成
mask = Z > 7
Z[mask] = 0
# プロットの準備
plt.subplot(2, 2, idx) # 2x2のサブプロットのidx番目を選択
idx += 1
plt.plot(x_history, y_history, 'o-', color="red") # パラメータの更新履歴をプロット
plt.contour(X, Y, Z) # 関数fの等高線をプロット
plt.ylim(-10, 10)
plt.xlim(-10, 10)
plt.plot(0, 0, '+') # 最小値を示すプラスマークをプロット
plt.title(key) # タイトルに最適化手法の名前を表示
plt.xlabel("x") # x軸ラベル
plt.ylabel("y") # y軸ラベル
# 全てのサブプロットを表示
plt.show()
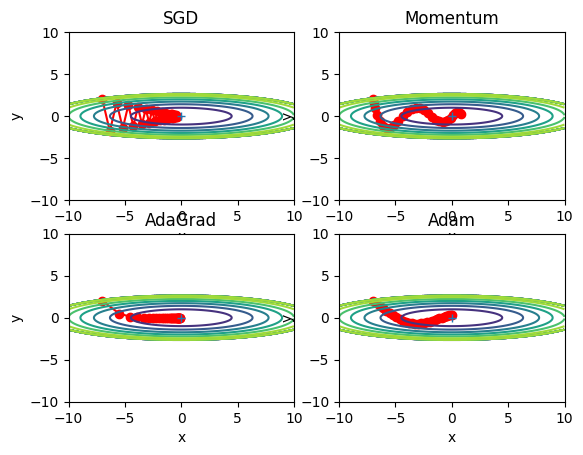
機械学習でよく使われる最適化アルゴリズムであるSGD(確率的勾配降下法)、Momentum、AdaGrad、Adamの振る舞いを比較するためのものです。それぞれの最適化アルゴリズムは、特定の関数を最小化するために使用されます。
まず、4つの最適化アルゴリズムがそれぞれクラスとして定義されています。それぞれのクラスは、学習率(lr)やその他のパラメータを初期化し、updateメソッドを持っています。updateメソッドは、パラメータの勾配に基づいてパラメータを更新します。
次に、最小化したい関数 f(x, y) とその勾配 df(x, y) が定義されています。この例では、二次関数が使用されています。
その後、各最適化アルゴリズムを用いて30回パラメータ更新を行います。パラメータの初期位置は init_pos で設定されています。それぞれの更新後のパラメータの位置(’x’と’y’)は x_history と y_history に保存されます。
最後に、各最適化アルゴリズムによるパラメータの更新の履歴を2次元の等高線グラフで描画します。ここで、’x’と’y’の値の履歴は赤色の線で描かれ、更新の経過が視覚的にわかるようになっています。
比較結果
SGD、Momentum、AdaGrad、Adamという4つの異なる最適化アルゴリズムが、2次元関数(この場合は f(x, y) = x**2 / 20.0 + y**2)の最小値を探索する様子を比較しています。これらのアルゴリズムは、初期位置から始めて、関数の勾配(傾き)を使用して最小値に向かって「移動」します。
具体的な結果は、実際にコードを実行して視覚化しなければ確認できませんが、各アルゴリズムの一般的な性質については以下のように考察できます:
- SGD(確率的勾配降下法): これは最も基本的な最適化手法で、各パラメータをその勾配方向に一定量(学習率)だけ移動させます。SGDは一般的にはうまく機能しますが、学習率が高すぎると、最適値の周りを振動する可能性があります。また、学習率が低すぎると、収束に時間がかかるか、局所最適値に陥る可能性があります。
- Momentum: MomentumはSGDに物理学の概念を導入し、パラメータが「運動量」を持つと考えます。これにより、最適化は一定方向に一貫して進むため、不必要な振動が減少し、収束が早くなる可能性があります。
- AdaGrad: AdaGradは学習率を動的に調整し、過去の勾配の大きさに基づいてそれぞれのパラメータの学習率を個別に調整します。これにより、学習率の手動調整の必要性が減少します。しかし、学習が進むにつれて学習率が過度に減少し、学習が早く停止する可能性があるため注意が必要です。
- Adam: AdamはMomentumとAdaGradのアイデアを組み合わせた方法で、適応的な学習率調整と運動量の概念を同時に利用します。これにより、さまざまな問題に対して一貫して良好な性能を発揮します。
どの最適化アルゴリズムが最良であるかは問題依存です。一部の問題ではSGDが適しているかもしれませんが、他の問題ではAdamが最良の結果をもたらすかもしれません。したがって、最適なアルゴリズムとパラメータを見つけるためには、通常、複数のアルゴリズムとパラメータ設定を試すことが必要です。
MNISTデータセットによる比較
MNISTデータセットによる比較を実装します。
import numpy as np # 数値計算を行うためのライブラリ
from collections import OrderedDict # 順序付きディクショナリを使用するためのライブラリ
import matplotlib.pyplot as plt # グラフ描画を行うためのライブラリ
# 多層のニューラルネットワークを定義するクラス
class MultiLayerNet:
# 初期化関数
# input_size: 入力層のノード数
# hidden_size_list: 隠れ層のノード数のリスト(隠れ層の数はリストの長さで決まる)
# output_size: 出力層のノード数
# activation: 活性化関数の種類('sigmoid'または'relu')
# weight_init_std: 重みの初期化時の標準偏差
# weight_decay_lambda: 重み減衰を制御するパラメータ(L2正則化)
def __init__(self, input_size, hidden_size_list, output_size,
activation='relu', weight_init_std='relu', weight_decay_lambda=0):
# 引数をインスタンス変数に格納
self.input_size = input_size
self.output_size = output_size
self.hidden_size_list = hidden_size_list
self.hidden_layer_num = len(hidden_size_list)
self.weight_decay_lambda = weight_decay_lambda
self.params = {} # 重みとバイアスを格納するためのディクショナリ
# 重みの初期化
self.__init_weight(weight_init_std)
# 活性化関数の層を設定
activation_layer = {'sigmoid': Sigmoid, 'relu': Relu}
self.layers = OrderedDict() # 順序付きディクショナリ(順序が重要なので通常のディクショナリではなく、順序付きディクショナリを使用)
for idx in range(1, self.hidden_layer_num+1):
# Affine層(全結合層)の追加
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)])
# 活性化関数層の追加
self.layers['Activation_function' + str(idx)] = activation_layer[activation]()
# 出力層のAffine層の追加
idx = self.hidden_layer_num + 1
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)])
# 最後の層(Softmax-with-Loss層)の設定
self.last_layer = SoftmaxWithLoss()
# 重みの初期化
# 重みの初期化を行うメソッド
def __init_weight(self, weight_init_std):
# 全ての層のノード数のリストを作成(入力層、隠れ層、出力層)
all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
for idx in range(1, len(all_size_list)):
scale = weight_init_std
if str(weight_init_std).lower() in ('relu', 'he'):
# ReLUまたはHeの初期値を用いる場合
scale = np.sqrt(2.0 / all_size_list[idx - 1])
elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
# SigmoidまたはXavierの初期値を用いる場合
scale = np.sqrt(1.0 / all_size_list[idx - 1])
# 重み(W)とバイアス(b)の初期化
self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx])
self.params['b' + str(idx)] = np.zeros(all_size_list[idx])
# 予測を行うメソッド
def predict(self, x):
# 各層を順に通過させる(順伝播)
for layer in self.layers.values():
x = layer.forward(x)
return x
# 損失関数の値(交差エントロピー誤差 + 重み減衰項)を計算するメソッド
def loss(self, x, t):
# 予測値の計算
y = self.predict(x)
# 重み減衰項(L2正則化)の計算
weight_decay = 0
for idx in range(1, self.hidden_layer_num + 2):
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
# 損失関数の値を計算(交差エントロピー誤差 + 重み減衰項)
return self.last_layer.forward(y, t) + weight_decay
# 認識精度を計算するメソッド
def accuracy(self, x, t):
# 予測値の計算
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1 : t = np.argmax(t, axis=1)
# 認識精度の計算
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# 勾配を数値的に計算するメソッド(確認用)
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
for idx in range(1, self.hidden_layer_num+2):
grads['W' + str(idx)] = numerical_gradient(loss_W, self.params['W' + str(idx)])
# バイアスの勾配の計算
grads['b' + str(idx)] = numerical_gradient(loss_W, self.params['b' + str(idx)])
# 勾配のディクショナリを返す
return grads
# 勾配を誤差逆伝播法で計算するメソッド
def gradient(self, x, t):
# 順伝播
self.loss(x, t)
# 逆伝播
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse() # 逆順にする(逆伝播なので)
for layer in layers:
dout = layer.backward(dout)
# 勾配を保存するためのディクショナリ
grads = {}
for idx in range(1, self.hidden_layer_num+2):
# 重みとバイアスの勾配を計算し、ディクショナリに保存
grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.layers['Affine' + str(idx)].W
grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db
# 勾配のディクショナリを返す
return grads
# SGDクラス: Stochastic Gradient Descentの実装
class SGD:
def __init__(self, lr=0.01):
# 学習率の初期化
self.lr = lr
def update(self, params, grads):
# すべてのパラメータについて、勾配に学習率を掛けて更新する
for key in params.keys():
params[key] -= self.lr * grads[key]
# Momentumクラス: Momentum SGDの実装
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
# 学習率とモメンタム係数の初期化
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
# 初回呼び出し時にモメンタムをパラメータと同じ形状で初期化する
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
# パラメータの更新
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]
# AdaGradクラス: AdaGradの実装
class AdaGrad:
def __init__(self, lr=0.01):
# 学習率の初期化
self.lr = lr
self.h = None
def update(self, params, grads):
# 初回呼び出し時にhをパラメータと同じ形状で初期化する
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
# パラメータの更新
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
# Adamクラス: Adamの実装
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
# 初回呼び出し時にmとvをパラメータと同じ形状で初期化する
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
# パラメータの更新
for key in params.keys():
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
# Sigmoidクラス: Sigmoid関数の実装
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = sigmoid(x)
self.out = out
return out
def backward(self, dout):
# Sigmoid関数の微分を計算
dx = dout * (1.0 - self.out) * self.out
return dx
# Reluクラス: Rectified Linear Unit関数の実装
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
# 順伝播では、0以下を0にする
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
# 逆伝播では、順伝播時に0以下だった部分は逆伝播の際にも0にする
dout[self.mask] = 0
dx = dout
return dx
# Affineクラス: 全結合層(Affineレイヤ)の実装
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.original_x_shape = None
self.dW = None
self.db = None
def forward(self, x):
# 入力の形状を記憶(テンソル対応)
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
# 順伝播の計算
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
# 逆伝播の計算
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape)
return dx
# SoftmaxWithLossクラス: Softmax関数とクロスエントロピー誤差を組み合わせたレイヤの実装
class SoftmaxWithLoss:
def __init__(self):
self.loss = None
self.y = None
self.t = None
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
# バッチの数で正規化して、上流から伝わった微分値(dout)を乗じる
batch_size = self.t.shape[0]
if self.t.size == self.y.size:
dx = (self.y - self.t) / batch_size
else:
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx = dx / batch_size
return dx
# softmax関数
def softmax(x):
x = x - np.max(x, axis=-1, keepdims=True) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x), axis=-1, keepdims=True)
# クロスエントロピー誤差の計算
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
# データの平滑化(グラフの描画を滑らかにするため)
def smooth_curve(x):
window_len = 11
s = np.r_[x[window_len-1:0:-1], x, x[-1:-window_len:-1]]
w = np.kaiser(window_len, 2)
y = np.convolve(w/w.sum(), s, mode='valid')
return y[5:len(y)-5]
# KerasからMNISTデータセットをインポート
from keras.datasets import mnist
# データセットのロードと前処理(正規化)
(x_train, t_train), (x_test, t_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
# 訓練データの数、バッチサイズ、最大イテレーション数を設定
train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000
# 最適化手法を辞書に格納
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
# 各最適化手法に対応するネットワークと訓練損失リストを作成
networks = {}
train_loss = {}
for key in optimizers.keys():
networks[key] = MultiLayerNet(
input_size=784, hidden_size_list=[100, 100, 100, 100],
output_size=10)
train_loss[key] = []
# バッチを選択し、各最適化手法でネットワークを更新
for i in range(max_iterations):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for key in optimizers.keys():
grads = networks[key].gradient(x_batch, t_batch)
optimizers[key].update(networks[key].params, grads)
loss = networks[key].loss(x_batch, t_batch)
train_loss[key].append(loss)
if i % 100 == 0:
print( "===========" + "iteration:" + str(i) + "===========")
for key in optimizers.keys():
loss = networks[key].loss(x_batch, t_batch)
print(key + ":" + str(loss))
# 各最適化手法の訓練損失をプロット
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()出力結果:
===========iteration:0===========
SGD:2.4276812394863434
Momentum:2.4516900768248786
AdaGrad:2.035472182320865
Adam:2.192773885963459
===========iteration:100===========
SGD:1.594728870092728
Momentum:0.4863079555841739
AdaGrad:0.23163925508774433
Adam:0.35776769812400777
===========iteration:200===========
SGD:0.8506934692946964
Momentum:0.344054941938905
AdaGrad:0.15595700108962499
Adam:0.3214382211442086
===========iteration:300===========
SGD:0.5630854823663645
Momentum:0.254818908059543
AdaGrad:0.0933754895808952
Adam:0.16994710686622744
===========iteration:400===========
SGD:0.5322213104451474
Momentum:0.1488557980910587
AdaGrad:0.06255881550699702
Adam:0.12754309315174284
===========iteration:500===========
SGD:0.45566960092583597
Momentum:0.11202970452118899
AdaGrad:0.04593273376227268
Adam:0.052314645774982516
===========iteration:600===========
SGD:0.3672510321264767
Momentum:0.10123753725508124
AdaGrad:0.05720804612048199
Adam:0.09391926577341655
===========iteration:700===========
SGD:0.3578586337332641
Momentum:0.09517419623925397
AdaGrad:0.025034887545030745
Adam:0.03185441206982659
===========iteration:800===========
SGD:0.38498777345456403
Momentum:0.1508345475796861
AdaGrad:0.14330774347747016
Adam:0.09320873545503774
===========iteration:900===========
SGD:0.328788654706481
Momentum:0.2192815674061278
AdaGrad:0.09277974142229845
Adam:0.13373468853679854
===========iteration:1000===========
SGD:0.1836186817975457
Momentum:0.05137026845914548
AdaGrad:0.01698048638404168
Adam:0.022523844532702595
===========iteration:1100===========
SGD:0.13802783987029946
Momentum:0.02733474129324303
AdaGrad:0.01269158701029086
Adam:0.04461366616936174
===========iteration:1200===========
SGD:0.32972164650737484
Momentum:0.20227614077261627
AdaGrad:0.049148516058627176
Adam:0.08231145980905599
===========iteration:1300===========
SGD:0.2410041636847441
Momentum:0.10391665030563743
AdaGrad:0.036053594041144214
Adam:0.06535536709423506
===========iteration:1400===========
SGD:0.2946729828620252
Momentum:0.10139350873397797
AdaGrad:0.022150341301949136
Adam:0.03501532152601983
===========iteration:1500===========
SGD:0.37729490517339925
Momentum:0.12300667722232045
AdaGrad:0.07028989289480675
Adam:0.06323167939418362
===========iteration:1600===========
SGD:0.26599572494998275
Momentum:0.09616328682309455
AdaGrad:0.050871585124355995
Adam:0.10215028480467724
===========iteration:1700===========
SGD:0.4016358325065463
Momentum:0.16849667400353546
AdaGrad:0.07189490323423726
Adam:0.07987638328663768
===========iteration:1800===========
SGD:0.25003700025529596
Momentum:0.0877659547062771
AdaGrad:0.04389859591163443
Adam:0.06355017964925018
===========iteration:1900===========
SGD:0.24675687855545167
Momentum:0.09687066772334499
AdaGrad:0.048686855263636225
Adam:0.06846785554991137まず、MultiLayerNetクラスは、ディープラーニングのモデルの一種である多層パーセプトロン(MLP)を定義しています。MLPは入力層、隠れ層、出力層の3つの層から構成され、各層は複数のニューロン(ユニット)で構成されます。MultiLayerNetクラスの__init__メソッドでは、モデルの各層の初期化が行われています。
次に、SGD, Momentum, AdaGrad, Adamというクラスは、それぞれ異なる最適化手法を表しています。これらはモデルの学習に用いられ、パラメータ(重みとバイアス)の更新方法を定義しています。このコードでは、これら4つの異なる最適化手法を同時に比較しています。
その後、MNISTデータセットを読み込み、それを使ってネットワークの学習を行っています。ここでは、各最適化手法で訓練したネットワークのパフォーマンスを比較しています。
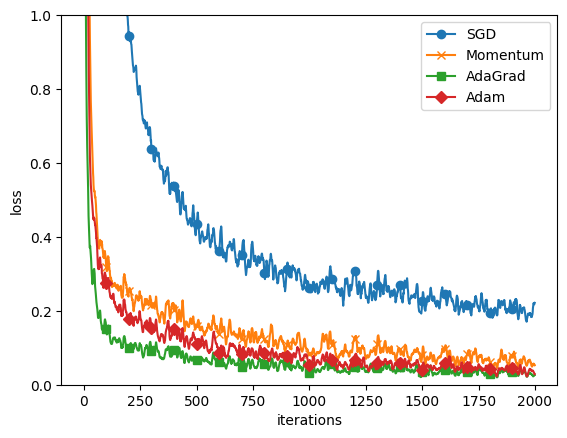
最後に、各最適化手法の学習曲線(損失関数の値をプロット)を表示します。これにより、各最適化手法がどの程度うまく学習できたか(損失がどれだけ減少したか)を視覚的に比較することができます。
まとめ
最後までご覧いただきありがとうございました。

