このシリーズではE資格対策として、シラバスの内容を項目別にまとめています。
教師なし学習
教師なし学習の概要
教師なし学習は、ラベルが付けられていないデータからパターンや構造を見つけ出す機械学習の一種です。教師あり学習と異なり、教師なし学習では正解ラベルが提供されず、アルゴリズム自体がデータの内部構造を理解しようとします。
教師なし学習の一つの重要な手法が「クラスタリング」です。クラスタリングは、データを自然なグループまたは「クラスタ」に分割するために使用されます。各クラスタは、その中に含まれるデータポイントが互いに似ていて、他のクラスタのデータポイントとは異なるという特性を持ちます。人気のあるクラスタリングアルゴリズムには、K-meansや階層的クラスタリングなどがあります。
教師なし学習の別の重要な手法は「次元削減」です。次元削減は、データの特徴の数を減らすことで、データをより簡単に理解しやすくします。この手法は、主成分分析(PCA)などの技術を用いて、データの情報を損失することなく特徴量を減らすことができます。
「異常検知」は、データ中の異常値や外れ値を検出する手法です。これは通常、正常なパターンから大きく逸脱したデータポイントを見つけるために使用されます。
「密度推定」は、データがどのように空間上に分布しているかを理解するための手法です。これは、特定の領域内のデータポイントの存在確率を推定することにより、データの全体的な構造を明らかにします。
k-means
k-meansはクラスタリングと呼ばれる手法の一つです。
クラスタリングとは、データを特徴に基づいてグループに分けることを意味します。例えば、店舗の顧客データがあったとします。その顧客データを年齢、購入頻度、好きな商品のカテゴリなどの特徴に基づいてグループに分けることができます。これにより、似た特徴を持つ顧客群を識別し、それぞれに対するマーケティング戦略を考えることができます。
k-meansは、そのようなクラスタリングを行うための簡単で効率的な手法です。k-meansのkは、クラスタの数を示します。つまり、k=3なら、データを3つのグループに分けることを目指します。
k-meansの手法は以下のように動作します。
- まず、データセットからランダムにk個のデータ点を選び出し、それぞれをクラスタの初期の「中心点」とします。
- 次に、残りの各データ点について、選ばれたk個の中心点のうち最も近いものを求めます。この「近さ」を測るために、一般的にはユークリッド距離が用いられます。
- それぞれのデータ点が最も近い中心点に基づいてクラスタに割り当てられたら、次に、それぞれのクラスタの中心点を再計算します。新しい中心点は、そのクラスタに属するデータ点の平均値(つまり「重心」)となります。
- このプロセスを、中心点が変化しなくなるか、あるいは設定した繰り返し回数に達するまで繰り返します。
k-meansの実装
k-meansによるクラスタリングを実装します。ランダムな初期重心を設定し、その後、データ点と重心との距離を計算し、各データポイントを最も近い重心が持つクラスタに割り当てます。次に、新たなクラスタ重心を計算します。これらのステップを新しいクラスタ割り当てが変わらなくなるか、あるいは最大イテレーション数に達するまで繰り返します。
import numpy as np
import matplotlib.pyplot as plt
def init_centroid(X, n_data, k):
# 各データ点の中からクラスタの重心となる点をk個ランダムに選択
idx = np.random.permutation(n_data)[:k]
centroids = X[idx]
return centroids
def compute_distances(X, k, n_data, centroids):
distances = np.zeros((n_data, k))
for idx_centroids in range(k):
dist = np.sqrt(np.sum((X - centroids[idx_centroids]) ** 2, axis=1))
distances[:, idx_centroids] = dist
return distances
def k_means(k, X, max_iter=300):
"""
X.shape = (データ数, 次元数)
k = クラスタ数
"""
n_data, n_features = X.shape
# 重心の初期値
centroids = init_centroid(X, n_data, k)
# 新しいクラスタを格納するための配列
new_cluster = np.zeros(n_data)
# 各データの所属クラスタを保存する配列
cluster = np.zeros(n_data)
for epoch in range(max_iter):
# 各データ点と重心との距離を計算
distances = compute_distances(X, k, n_data, centroids)
# 新たな所属クラスタを計算
new_cluster = np.argmin(distances, axis=1)
# すべてのクラスタに対して重心を再計算
for idx_centroids in range(k):
centroids[idx_centroids] = X[new_cluster == idx_centroids].mean(axis=0)
# クラスタによるグループ分けに変化がなかったら終了
if (new_cluster == cluster).all():
break
cluster = new_cluster
return cluster
# データ数と特徴量の数を指定
n_data = 100
n_features = 2
# ランダムな値でデータを生成
X = np.random.rand(n_data, n_features)
# クラスタ数を指定
k = 3
# k-meansアルゴリズムを実行
cluster = k_means(k, X)
# クラスタリング結果をプロット
for i in range(k):
plt.scatter(X[cluster == i, 0], X[cluster == i, 1])
plt.show()実行結果:
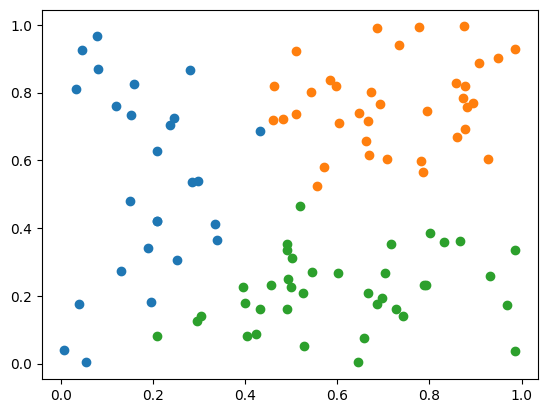
n_data個のn_features次元のデータをランダムに生成し、それを用いてk-meansクラスタリングを実行。そして、各クラスタのデータポイントを別々の色でプロットして、クラスタリング結果を可視化します。
k-means++
k-means++は、データクラスタリングを目的とするk-meansアルゴリズムの初期化手法の一つです。この手法は、初期のクラスタ中心を適切に選択することで、k-meansアルゴリズムの結果の品質を改善し、計算時間を短縮します。
k-means++のアルゴリズムは次のように行われます:
- 最初のクラスタ中心はデータセットからランダムに選ばれます。
- 次に、それぞれのデータ点から最も近いクラスタ中心までの距離を計算します。これは、データ点がどのクラスタに所属するかを決定するための基準となります。
- ここで、ルーレット選択が登場します。ルーレット選択とは、ある確率に基づき次のクラスタ中心を選択する手法です。各データ点が新しいクラスタ中心として選ばれる確率は、そのデータ点から既存のクラスタ中心までの距離に比例します。つまり、遠くのデータ点ほど新しいクラスタ中心として選ばれやすくなります。
- 上記の手順をk個のクラスタ中心が選ばれるまで繰り返します。
このように、k-means++では初期クラスタ中心の選択にルーレット選択を用いることで、データの分布をよりよく反映し、k-meansアルゴリズムのクラスタリング結果の品質と効率性を向上させることが期待されます。
k-means++の実装
k-means++法を用いてデータセットから初期のクラスタ中心を選択します。この方法では、最初のクラスタ中心はランダムに選択され、次のクラスタ中心は既存のクラスタ中心からの距離に比例した確率で選択されます。これにより、クラスタ中心がデータセット内で均等に分散され、k-means法の収束速度が向上します。
# 必要なライブラリをインポートします。numpyは数値計算、matplotlib.pyplotはグラフ描画のためです。
import numpy as np
import matplotlib.pyplot as plt
# データとセントロイド間の距離を計算する関数を定義します。
def compute_distances(X, k, n_data, centroids):
# 各データポイントと各セントロイド間の距離を格納するための配列を初期化します。
distances = np.zeros((n_data, k))
# 各セントロイドについて距離を計算します。
for idx_centroids in range(k):
# データとセントロイドの距離(ユークリッド距離)を計算します。
dist = np.sqrt(np.sum((X - centroids[idx_centroids]) ** 2, axis=1))
# 計算した距離を距離配列に保存します。
distances[:, idx_centroids] = dist
return distances
# 初期のセントロイドをランダムに選択する関数を定義します。
def init_centroid(X, n_data, k):
# データのインデックスからランダムに1つ選び、最初のセントロイドとします。
idx = np.random.choice(n_data, 1)
centroids = X[idx]
# 残りのセントロイドを選択します。
for i in range(k - 1):
# 既に選ばれたセントロイドとデータ点の距離を計算します。
distances = compute_distances(X, len(centroids), n_data, centroids)
# 各データ点について、最も近いセントロイドまでの距離を計算します。
closest_dist_sq = np.min(distances ** 2, axis=1)
# 距離の合計を計算します。
weights = closest_dist_sq.sum()
# ランダムな値を生成し、その値に応じたデータ点を新たなセントロイドとして選択します。
rand_vals = np.random.random_sample() * weights
candidate_ids = np.searchsorted(np.cumsum(closest_dist_sq), rand_vals)
centroids = np.vstack([centroids, X[candidate_ids]])
return centroids
# データポイントと特徴量の数を設定します。
n_data = 100
n_features = 2
# セントロイドの数(クラスタの数)を設定します。
k = 3
# データをランダムに生成します。
X = np.random.rand(n_data, n_features)
# 初期のセントロイドを選択します。
centroids = init_centroid(X, n_data, k)
# データポイントを散布図にプロットします。
plt.scatter(X[:, 0], X[:, 1])
# セントロイドを赤色でプロットします。
plt.scatter(centroids[:, 0], centroids[:, 1], c='red')
# グラフのタイトルを設定します。
plt.title('Data Points and Initial Centroids')
# 凡例を追加します。
plt.legend()
# グラフを表示します。
plt.show()実行結果:
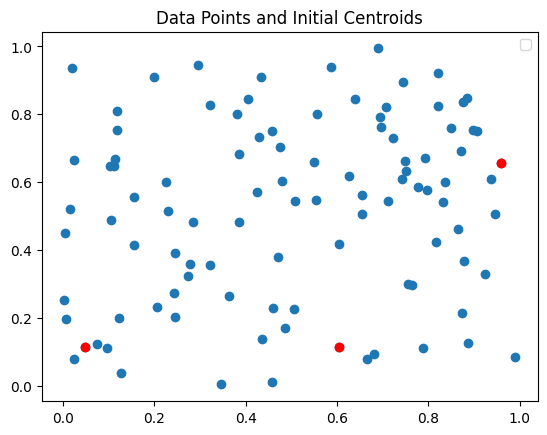
初期のセントロイドを選択した後、各データポイントを最も近いセントロイドのクラスタに割り当て、その後セントロイドを更新するという手順を繰り返します。ただし、ここでは初期のセントロイドを選択する部分と、それをプロットする部分のみを実装しています。
主成分分析
主成分分析(PCA)は、高次元データの情報を可能な限り多く保持しながらデータをより少ない次元に「削減」するための手法です。この技術は「次元削減」技術の一種としてよく用いられます。
具体的には、元の変数が持つ情報をできるだけ失わないように、新たな座標系を作成しデータを再配置します。その新たな座標系の軸が、主成分と呼ばれるものです。主成分はデータの分散が最大となる方向を示しており、そのために我々は分散共分散行列を利用します。
分散共分散行列とは、各変数の分散と共分散をまとめた行列です。分散は変数がどれだけ散らばっているかを表し、共分散は2つの変数がどれだけ同時に変動するかを示します。この行列を用いて、データの散らばり方を最大化する方向を見つけ出すことが可能になります。
この分散共分散行列を解析することで、固有ベクトルと固有値が得られます。固有ベクトルはデータが散らばる方向を示し、その長さが固有値で決まります。固有値が大きいほどその方向への散らばりが大きいと考えることができます。
そして、それぞれの主成分がデータ全体の情報をどの程度保持しているかを表す指標が寄与率です。寄与率は各主成分の固有値を全固有値の和で割ったもので、この値が大きいほどその主成分がもとのデータの情報を多く含んでいると言えます。
主成分分析の実装
import numpy as np # NumPy ライブラリを読み込む。科学計算を行うためのライブラリ。
# PCA (主成分分析)を行う関数
def pca(X, n_components=2):
X = X - X.mean(axis=0) # データから平均を引いてデータを正規化する
cov = np.cov(X, rowvar=False) # データの共分散行列を計算する
l, v = np.linalg.eig(cov) # 共分散行列の固有値と固有ベクトルを計算する
l_index = np.argsort(l)[::-1] # 固有値を大きい順に並べ替え、そのインデックスを取得する
v_ = v[:,l_index] # 固有ベクトルを固有値の大きい順に並べ替える
components = v_[:,:n_components] # 最も大きいn個の固有ベクトル(主成分)を取得する
T = np.dot(X, components) # 元のデータを主成分に射影する
return T # 射影されたデータを返す
# ランダムなデータセットの生成
np.random.seed(0) # 乱数のシードを設定する。これにより、同じ結果を再現できる。
X = np.random.rand(10, 5) # 10x5の行列の各要素を0~1の間のランダムな数値で埋める
# 入力データの表示
print("Input Data:") # "Input Data:"と表示する
print(X) # 入力データを表示する
# PCA の実行
result = pca(X, n_components=2) # pca関数を使って、2つの主成分を持つデータに変換する
# 結果の表示
print("\nOutput Data:") # "\nOutput Data:"と表示する。"\n"は改行を意味する。
print(result) # 主成分分析の結果を表示する実行結果:
import numpy as np
# PCA 関数
def pca(X, n_components=2):
X = X - X.mean(axis=0)
cov = np.cov(X, rowvar=False)
l, v = np.linalg.eig(cov)
l_index = np.argsort(l)[::-1]
v_ = v[:,l_index]
components = v_[:,:n_components]
…
# PCA の実行
result = pca(X, n_components=2)
# 結果の表示
print("\nOutput Data:")
print(result)
Input Data:
[[0.5488135 0.71518937 0.60276338 0.54488318 0.4236548 ]
[0.64589411 0.43758721 0.891773 0.96366276 0.38344152]
[0.79172504 0.52889492 0.56804456 0.92559664 0.07103606]
[0.0871293 0.0202184 0.83261985 0.77815675 0.87001215]
[0.97861834 0.79915856 0.46147936 0.78052918 0.11827443]
[0.63992102 0.14335329 0.94466892 0.52184832 0.41466194]
[0.26455561 0.77423369 0.45615033 0.56843395 0.0187898 ]
[0.6176355 0.61209572 0.616934 0.94374808 0.6818203 ]
[0.3595079 0.43703195 0.6976312 0.06022547 0.66676672]
[0.67063787 0.21038256 0.1289263 0.31542835 0.36371077]]
Output Data:
[[-0.09150808 0.10412935]
[-0.03471536 -0.41757135]
[-0.42427325 -0.19299645]
[ 0.76549898 -0.26305905]
[-0.62059276 -0.02702175]
[ 0.26488503 -0.09145729]
[-0.27959735 0.24832636]
[-0.01023595 -0.29202606]
[ 0.4358998 0.43832102]
[-0.00536107 0.49335522]]次元の呪い
次元の呪いとは、データの次元数が増えるにつれて、データを正確に捉えるために必要な計算量やサンプルサイズが指数関数的に増大するという問題です。この現象は、特に高次元空間におけるデータの分布や、その扱いに困難をもたらします。次元が増えるとデータ間の距離も増大し、データポイントがスパースになります。これは、学習アルゴリズムが適切なモデルを見つけるのを難しくし、結果として精度が低下します。
この次元の呪いは、球面集中現象と密接に関連しています。高次元空間では、体積の大部分が表面(すなわち、球の「表皮」)に集中します。これは我々の直感とは大きく異なり、機械学習モデルの訓練や評価に影響を与えます。データが高次元空間の球面上に分散してしまうと、予測モデルの学習は困難を極め、データがスパースになります。
この問題を克服するための一つの方法が「特徴選択」です。特徴選択は、データセットの次元数を減らすための手法であり、不要な特徴を取り除くことで、モデルの予測精度を向上させると同時に、計算効率も向上させます。特徴選択は、データの解釈性を保つためにも重要な役割を果たします。
特徴選択の手法は多様で、フィルタ法、包含法、組み合わせ法などがあります。フィルタ法は、特徴間の統計的な関連性を計算し、最も有用な特徴を選び出します。包含法は、機械学習モデルの訓練と特徴選択を同時に行う手法で、特徴のセットが予測性能にどのように影響するかを直接的に評価します。組み合わせ法は、フィルタ法と包含法の両方を組み合わせて、最も効果的な特徴セットを選択します。
まとめ
最後までご覧いただきありがとうございました。

