このシリーズではE資格対策として、シラバスの内容を項目別にまとめています。
E資格まとめ
試験概要 ディープラーニングの理論を理解し、適切な手法を選択して実装する能力や知識を有しているかを認定する。 １．応用数学 （１）確率・統計 （２）情報理論 ２．機…
つくもちブログ 〜Python&AIまとめ〜 混同行列
混同行列とは
混同行列（Confusion Matrix）は、分類モデルの性能を評価するために使用される表です。分類モデルは、データを特定のカテゴリに分類することを目的としており、例えばスパムメールの検出や病気の診断などが挙げられます。
混同行列は、モデルが予測した結果と実際の正解（正解ラベル）を比較して、予測がどの程度正確であるかを示すものです。この表には、通常、以下の4つの要素が含まれます。
- 真陽性 (True Positive, TP)
- 偽陽性 (False Positive, FP)
- 真陰性 (True Negative, TN)
- 偽陰性 (False Negative, FN)
これらの要素を使って、分類モデルの性能を評価する指標（正確度、適合率、再現率、F1スコアなど）を計算します。混同行列を理解することで、モデルの弱点や改善点を把握し、より高い性能を持つモデルを開発することができます。
なぜ混同行列が重要なのか？
混同行列が重要である理由は、以下のような点が挙げられます。
- モデルの性能を定量的に評価: 混同行列を使用することで、モデルの予測結果を正確に把握し、定量的に評価することができます。これにより、モデルの改善やチューニングが容易になります。
- 複数の評価指標を提供: 混同行列を基に、正確度、適合率、再現率、F1スコアなど、さまざまな評価指標を計算することができます。これにより、特定の指標だけに頼らず、モデルの性能を総合的に判断できます。
- クラスごとの性能を把握: 混同行列は、各クラス（カテゴリ）ごとの予測結果を明確に示すため、モデルが特定のクラスに対してどのような性能を発揮しているかを理解することができます。
- モデルの弱点を特定: 混同行列を分析することで、モデルが過剰に陽性結果を予測しているのか、陰性結果を予測しているのか、または両方のバランスが取れているのかを判断できます。これにより、モデルの弱点や改善点を特定できます。
混同行列の構成要素
混同行列は、以下の4つの要素で構成されています。
a. 真陽性 (True Positive, TP): モデルが正しく陽性クラス（例: 病気）と予測し、実際に陽性クラスである場合。
b. 偽陽性 (False Positive, FP): モデルが誤って陽性クラスと予測し、実際には陰性クラス（例: 健康）である場合。これは、型Iエラーとも呼ばれます。
c. 真陰性 (True Negative, TN): モデルが正しく陰性クラスと予測し、実際に陰性クラスである場合。
d. 偽陰性 (False Negative, FN): モデルが誤って陰性クラスと予測し、実際には陽性クラスである場合。これは、型IIエラーとも呼ばれます。
これらの構成要素を使って、混同行列は以下のように表現されます。
| 予測: 病気 | 予測: 健康 | |
|---|---|---|
| 実際: 病気 | TP | FN |
| 実際: 健康 | FP | TN |
混同行列を使って評価指標を理解する
混同行列の構成要素を使用して、以下の評価指標を計算することができます。
正確率 (Accuracy)
モデルが全体としてどれだけ正確に予測できたかを示す指標です。真陽性（TP）と真陰性（TN）の割合を計算します。
適合率 (Precision)
陽性クラスと予測されたデータのうち、実際に陽性クラスであるものの割合を示す指標です。偽陽性（FP）が少ないことを重視します。
再現率 (Recall)
実際に陽性クラスであるデータのうち、正しく陽性クラスと予測されたものの割合を示す指標です。偽陰性（FN）が少ないことを重視します。
F1 スコア (F1 Score)
適合率と再現率の調和平均を取った指標で、両者のバランスを示します。適合率と再現率が共に高い場合に、F1 スコアも高くなります。
これらの評価指標を使って、モデルの性能を総合的に評価することができます。また、各指標の特性により、モデルがどのような誤りを犯しやすいか（偽陽性か偽陰性か）や、どの指標を重視するかによって、モデルの改善方針を決定することができます。
混同行列の実例: 病気の診断
混同行列を使って、病気の診断に関する分類モデルの評価を考えてみましょう。この例では、病気の有無を判断するモデルがあり、患者データをもとに病気か健康かを予測します。
まず、以下のような混同行列が与えられたとします。
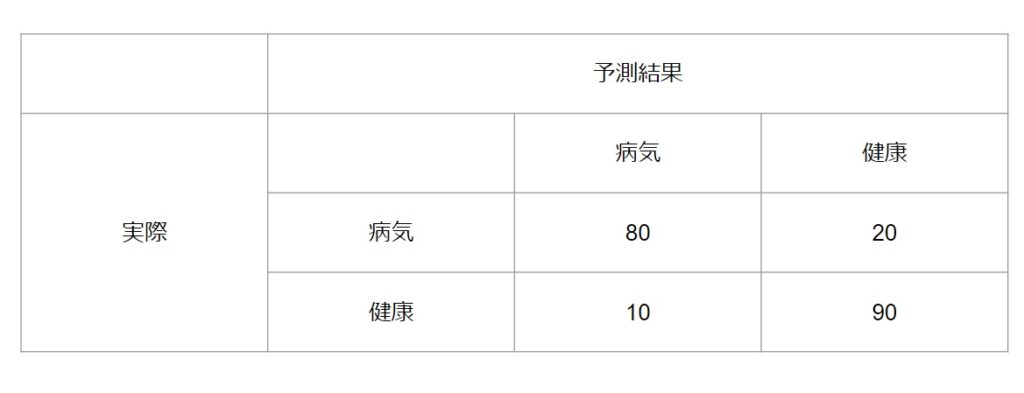
この混同行列から、以下の評価指標を計算できます。
- 正確率 (Accuracy): (80 + 90) / (80 + 20 + 10 + 90) = 0.85 (85%)
- 適合率 (Precision): 80 / (80 + 10) = 0.89 (89%)
- 再現率 (Recall): 80 / (80 + 20) = 0.8 (80%)
- F1 スコア (F1 Score): 2 * (0.89 * 0.8) / (0.89 + 0.8) = 0.84 (84%)
このモデルは、正確度が85%であり、全体的に正確な予測が行えていることが分かります。また、適合率が89%であり、病気と予測された患者のうち、89%が実際に病気であることが示されています。再現率が80%であり、実際に病気である患者のうち、80%が正しく病気と診断されています。F1スコアは84%であり、適合率と再現率のバランスが比較的良好であることが示されています。
混同行列の利点と欠点
混同行列は、分類モデルの評価において重要なツールですが、利点と欠点があります。
利点:
- 分類モデルの性能を定量的に評価できる。
- 複数の評価指標を提供し、モデルの性能を総合的に判断できる。
- クラスごとの性能を把握し、モデルの弱点や改善点を特定できる。
欠点:
- データの不均衡: クラス間でデータの分布が不均衡な場合、混同行列が示す性能評価が正確でないことがあります。例えば、あるクラスのデータが非常に少ない場合、正確度が高くても実際の性能が低いことがあります。このような場合、適合率、再現率、F1スコアなどの他の評価指標を使用することが重要です。
- 二値分類に限定される: 混同行列は基本的に二値分類の評価に使用されます。多クラス分類の場合、各クラスごとに二値分類問題として扱い、複数の混同行列を作成する必要があります。
混同行列は分類モデルの評価に有用ですが、データの不均衡や多クラス分類の問題に対処する際には注意が必要です。適切な評価指標を選択し、モデルの性能を総合的に判断することが重要です。
混同行列の実装
先ほどの病気診断を例に、Pythonを使用して混同行列から各評価指標を計算する簡単なコードを示します。
import numpy as np
from sklearn.metrics import confusion_matrix
# サンプルデータ (1: 病気, 0: 健康)
y_true = np.array([1, 0, 1, 1, 0, 1, 1, 0, 0, 0])
y_pred = np.array([1, 0, 1, 0, 0, 1, 1, 1, 0, 0])
# 混同行列の計算
cm = confusion_matrix(y_true, y_pred)
# 混同行列の構成要素
TP = cm[1, 1] # 真陽性 (True Positives)
FP = cm[0, 1] # 偽陽性 (False Positives)
TN = cm[0, 0] # 真陰性 (True Negatives)
FN = cm[1, 0] # 偽陰性 (False Negatives)
# 正確率 (Accuracy) の計算
accuracy = (TP + TN) / (TP + FP + TN + FN)
print("Accuracy:", accuracy)
# 適合率 (Precision) の計算
precision = TP / (TP + FP)
print("Precision:", precision)
# 再現率 (Recall) の計算
recall = TP / (TP + FN)
print("Recall:", recall)
# F1 スコア (F1 Score) の計算
f1_score = 2 * (precision * recall) / (precision + recall)
print("F1 Score:", f1_score)
病気の診断のサンプルデータ（y_true, y_pred）から混同行列を計算し、その要素（TP, FP, TN, FN）を取得します。次に、正確度、適合率、再現率、およびF1スコアを計算し、それらの値を表示します。コードを実行すると、以下のような結果が得られます。
実行結果:
Accuracy: 0.6
Precision: 0.6
Recall: 0.75
F1 Score: 0.6666666666666665まとめ
最後までご覧いただきありがとうございました。
