【E資格まとめ】VQ-VAE

このシリーズではE資格対策として、シラバスの内容を項目別にまとめています。

E資格まとめ

試験概要ディープラーニングの理論を理解し、適切な手法を選択して実装する能力や知識を有しているかを認定する。１．応用数学（１）確率・統計（２）情報理論２．機…

1. VQ-VAE
1.1. VQ-VAEの概要
1.2. VQ-VAEの特徴
1.3. VQ-VAEの活用事例
2. VQ-VAEの実装
3. まとめ

VQ-VAE

VQ-VAEの概要

Vector Quantized-Variational AutoEncoder (VQ-VAE) は、ディープラーニングを用いた生成モデルの一種で、変分オートエンコーダ（VAE）を拡張したモデルです。VQ-VAEの最大の特徴は、連続的な潜在空間を使用する代わりに、離散的な潜在空間を用いることにあります。

具体的には、エンコーダから出力された連続的な潜在変数を離散的な潜在ベクトルに変換します。この変換はベクトル量子化と呼ばれ、固定されたコードブック（ベクトルの集合）から最も近いベクトル（量子化ベクトル）を選択することで行います。そして、この量子化ベクトルがデコーダに渡され、オリジナルのデータに変換されます。

VQ-VAEは主にエンコーダ、量子化層、デコーダの3つの部分から成り立っています。

エンコーダ: 入力データ（画像や音声など）を低次元の特徴空間（潜在空間）にマッピングします。この過程は非線形変換を使用して行われ、その結果、潜在表現（潜在ベクトル）が得られます。
量子化層: この層では、潜在ベクトルが離散的な表現に変換されます。具体的には、事前に定義されたベクトルの集合（コードブック）から最も近いベクトル（コードワード）が選ばれ、そのインデックスが潜在ベクトルの代わりに使用されます。この量子化ステップにより、モデルはデータの離散的な表現を学習することが可能になります。
デコーダ: 最後に、量子化された潜在表現は、デコーダを通じて元のデータ空間にマッピングされます。デコーダは、量子化された表現から元のデータを再構築（デコード）します。

VQ-VAEの学習目的は、元のデータと再構成されたデータ間の再構成誤差と、潜在変数と選択された量子化ベクトル間の距離の和を最小化することです。また、コードブックのベクトルも学習過程で更新されます。

VQ-VAEの特徴

メリット：

離散的な潜在空間：VQ-VAEは、離散的な潜在空間を使用します。これにより、自然言語や画像などの離散的なデータに対する生成タスクに特に適しています。
学習が容易：VQ-VAEは、潜在空間が離散的であるため、KLダイバージェンス項を用いる必要がなく、学習が容易です。
ハイレゾリューションな生成：一部のアーキテクチャ（例：VQ-VAE-2）では、複数の階層を用いることで、よりハイレゾリューションな生成が可能です。

デメリット：

量子化誤差：潜在空間を離散化することで、元のデータと量子化されたデータとの間に一部の情報が失われる可能性があります。
コードブックの学習：コードブックのベクトルも学習過程で更新されるため、全体としての学習負荷が高くなる可能性があります。
モデルの複雑さ：VQ-VAEは一般的なVAEに比べてモデルが複雑であるため、設計と実装が難しい場合があります。

VQ-VAEの活用事例

画像生成：VQ-VAEは、学習した画像データから新たな画像を生成する能力があります。特に、ハイレゾリューションな画像生成において強いです。

音声合成：音声波形の生成にもVQ-VAEは用いられます。特にOpenAIのWaveNetでは、VQ-VAEを組み合わせることで高品質な音声合成を実現しています。

自然言語処理：VQ-VAEは離散的な潜在空間を使用するため、自然言語のような離散的なデータに対する処理に適しています。例えば、テキストデータの生成や変換タスクに使用することができます。

強化学習：VQ-VAEは環境の状態を離散的な潜在空間にエンコードすることで、強化学習の状態表現に使用することができます。これにより、環境の複雑な状態を効率的に表現することが可能になります。

VQ-VAEの実装

Vector Quantized Variational Autoencoders（VQ-VAE）をMNISTデータセットで実装したプログラムの解説です。

ライブラリとデータセットの準備：まず、PyTorchとその他の必要なライブラリをインポートし、MNISTデータセットをロードします。データセットは、28×28ピクセルの手書き数字の画像で構成されています。

データの前処理：データセットは、カスタムのDataSetクラスを使用して前処理されます。このクラスは、データをトレーニングおよびテストセットに分割し、データローダーを作成します。

VQ-VAEモデルの構造：VQ-VAEモデルは、以下の部分から構成されます。

Encoder: 入力画像を低次元の潜在表現に変換します。

Vector Quantizer: 潜在表現を離散化し、潜在空間の特定のベクトルにマップします。

Decoder: 潜在表現を再構築画像に変換します。

残差ブロック：このモデルでは、残差ブロック（ResidualLayerとResidualStackクラス）を使用しています。これらは、ネットワークの学習を助け、より深いアーキテクチャを可能にします。

学習プロセス：モデルは、最小二乗誤差とベクトル量子化の損失を組み合わせた損失関数で学習します。指定されたエポック数で学習を進め、トレーニングとテストの損失をログに記録します。

結果の可視化：学習の結果をプロットし、元の画像と再構築された画像を並べて表示します。これにより、モデルが画像をどのように再構築しているかを視覚的に評価できます。

# グラフをインラインで表示するためのマジックコマンド
%matplotlib inline

# 必要なライブラリをインポート
import numpy as np
from tqdm.notebook import tqdm
import matplotlib.pyplot as plt
import torch
from torch.nn import functional as F
from torch import nn, optim
import torchvision
from torch.utils.data import Dataset, DataLoader
from torchvision import transforms
from torchvision import datasets, transforms

# GPUが利用可能であればCUDAデバイスを使用し、そうでなければCPUを使用
if torch.cuda.is_available():
    device = 'cuda'
else:
    device = 'cpu'

# MNISTデータセットのダウンロードとトレーニング、テストデータの変換
train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transforms.ToTensor())
test_dataset = datasets.MNIST(root='./data', train=False, transform=transforms.ToTensor())

# トレーニングデータとテストデータの前処理
x_train = train_dataset.data.reshape(-1, 784).float() / 255
y_train = F.one_hot(train_dataset.targets, 10).float()
x_test = test_dataset.data.reshape(-1, 784).float() / 255
y_test = F.one_hot(test_dataset.targets, 10).float()

# カスタムデータセットクラスの定義
class DataSet(Dataset):
    def __init__(self, data, transform=False):
        self.X = data[0]
        self.y = data[1]
        self.transform = transform
    
    def __len__(self):
        return len(self.X)
    
    def __getitem__(self, index):
        img = self.X[index].view(28, 28)
        label = self.y[index]
        if self.transform:
            img = transforms.ToPILImage()(img)
            img = self.transform(img)
        return img, label

# 画像データの正規化のための変換関数を定義
transform = transforms.Compose(
    [transforms.ToTensor(),
     transforms.Normalize((0.5, ), (0.5, ))] 
)

# トレーニングデータとテストデータセットの作成
trainset = DataSet([x_train,y_train], transform=transform)
testset = DataSet([x_test,y_test], transform=transform)

# バッチサイズの定義とデータローダーの作成
batch_size = 256
trainloader = DataLoader(trainset, batch_size=batch_size, drop_last=True, shuffle=True, num_workers=0)
testloader = DataLoader(testset, batch_size=batch_size, drop_last=False, shuffle=False, num_workers=0)

# 残差層クラスの定義
class ResidualLayer(nn.Module):
    # コンストラクタで畳み込み層を定義
    def __init__(self, in_dim, h_dim, res_h_dim):
        super(ResidualLayer, self).__init__()
        self.res_block = nn.Sequential(
            nn.ReLU(True), 
            nn.Conv2d(in_dim, res_h_dim, kernel_size=3, stride=1, padding=1, bias=False),
            nn.ReLU(True),
            nn.Conv2d(res_h_dim, h_dim, kernel_size=1, stride=1, bias=False)
        )
    
    # フォワードパスで残差接続を適用
    def forward(self, x):
        x = x + self.res_block(x)
        return x

# 残差スタッククラスの定義
class ResidualStack(nn.Module):
    # コンストラクタで指定された数の残差層をスタック
    def __init__(self, in_dim, h_dim, res_h_dim, n_res_layers):
        super(ResidualStack, self).__init__()
        self.n_res_layers = n_res_layers
        self.stack = nn.ModuleList(
            [ResidualLayer(in_dim, h_dim, res_h_dim)]*n_res_layers)

    # フォワードパスでスタックを通過させる
    def forward(self, x):
        for layer in self.stack:
            x = layer(x)
        x = F.relu(x)
        return x

# エンコーダクラスの定義
class Encoder(nn.Module):
    # コンストラクタで畳み込み層と残差スタックを定義
    def __init__(self, in_dim, h_dim, n_res_layers, res_h_dim):
        super(Encoder, self).__init__()
        kernel = 4
        stride = 2
        self.conv_stack = nn.Sequential(
            nn.Conv2d(in_dim, h_dim // 2, kernel_size=kernel, stride=stride, padding=1),
            nn.ReLU(),
            nn.Conv2d(h_dim // 2, h_dim, kernel_size=kernel, stride=stride, padding=1),
            nn.ReLU(),
            nn.Conv2d(h_dim, h_dim, kernel_size=kernel-1, stride=stride-1, padding=1),
            ResidualStack(h_dim, h_dim, res_h_dim, n_res_layers)
        )

    # フォワードパスで画像を特徴ベクトルにエンコード
    def forward(self, x):
        return self.conv_stack(x)

# ベクトル量子化クラスの定義
class VectorQuantizer(nn.Module):
    # コンストラクタでエンベッディング層を定義
    def __init__(self, n_e, e_dim, beta):
        super(VectorQuantizer, self).__init__()
        self.n_e = n_e
        self.e_dim = e_dim
        self.beta = beta
        self.embedding = nn.Embedding(self.n_e, self.e_dim)
        self.embedding.weight.data.uniform_(-1.0 / self.n_e, 1.0 / self.n_e)

    # フォワードパスで入力ベクトルを最も近いエンベッディングベクトルに量子化
    def forward(self, z):
        z = z.permute(0, 2, 3, 1).contiguous()
        z_flattened = z.view(-1, self.e_dim)
        d = torch.sum(z_flattened**2, dim=1, keepdim=True) + \
            torch.sum(self.embedding.weight**2, dim=1) - 2 * \
            torch.matmul(z_flattened, self.embedding.weight.t())
        min_encoding_indices = torch.argmin(d, dim=1).unsqueeze(1)
        min_encodings = torch.zeros(
            min_encoding_indices.shape[0], self.n_e).to(device)
        min_encodings.scatter_(1, min_encoding_indices, 1)
        z_q = torch.matmul(min_encodings, self.embedding.weight).view(z.shape)
        loss = torch.mean((z.detach() - z_q)**2) + \
            self.beta * torch.mean((z - z_q.detach()) ** 2)
        z_q = z + (z_q - z).detach()
        z_q = z_q.permute(0, 3, 1, 2).contiguous()
        return loss, z_q, min_encodings, min_encoding_indices

# デコーダクラスの定義
class Decoder(nn.Module):
    # コンストラクタで逆畳み込み層と残差スタックを定義
    def __init__(self, in_dim, h_dim, n_res_layers, res_h_dim):
        super(Decoder, self).__init__()
        kernel = 4
        stride = 2
        self.inverse_conv_stack = nn.Sequential(
            nn.ConvTranspose2d(in_dim, h_dim, kernel_size=kernel-1, stride=stride-1, padding=1),
            ResidualStack(h_dim, h_dim, res_h_dim, n_res_layers),
            nn.ConvTranspose2d(h_dim, h_dim // 2, kernel_size=kernel, stride=stride, padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(h_dim//2, 1, kernel_size=kernel, stride=stride, padding=1)
        )

    # フォワードパスで特徴ベクトルから画像をデコード
    def forward(self, x):
        return self.inverse_conv_stack(x)

# VQ-VAEモデルクラスの定義
class VQVAE(nn.Module):
    # コンストラクタでエンコーダ、ベクトル量子化層、デコーダを定義
    def __init__(self, h_dim, res_h_dim, n_res_layers, n_embeddings, embedding_dim, beta):
        super(VQVAE, self).__init__()
        self.encoder = Encoder(1, h_dim, n_res_layers, res_h_dim)
        self.pre_quantization_conv = nn.Conv2d(h_dim, embedding_dim, kernel_size=1, stride=1)
        self.vector_quantization = VectorQuantizer(n_embeddings, embedding_dim, beta)
        self.decoder = Decoder(embedding_dim, h_dim, n_res_layers, res_h_dim)

    # フォワードパスで画像をエンコード、量子化、デコード
    def forward(self, x):
        z_e = self.encoder(x)
        z_e = self.pre_quantization_conv(z_e)
        embedding_loss, z_q, _ , _ = self.vector_quantization(z_e)
        x_hat = self.decoder(z_q)
        return embedding_loss, x_hat

# エポック数の定義
epoch = 0
max_epoch = 5

# VQ-VAEモデルのインスタンス作成
model = VQVAE(128, 32, 2, 512, 64, .25)

# 最適化アルゴリズムの定義
opt = optim.Adam(model.parameters(), lr=3e-4, betas=(0.5, 0.9))

# トレーニングとテストのロスを記録するリスト
train_loss_log=[]
test_loss_log=[]

# エポックごとのトレーニングとテストループ
for i in tqdm(range(epoch,max_epoch+1)):
    train_loss=0
    test_loss=0
    model=model.to(device)
    
    # トレーニングモードでモデルを設定
    model.train()
    for (img, _) in trainloader:
        img = img.to(device,dtype=torch.float)
        opt.zero_grad()
        embedding_loss, x_hat = model(img)
        recon_loss = nn.MSELoss()(x_hat, img)
        loss = recon_loss + embedding_loss
        train_loss += loss.item()
        loss.backward()
        opt.step()
    
    # 評価モードでモデルを設定
    model.eval()
    for (img_t, _) in testloader:
        img = img.to(device,dtype=torch.float)
        embedding_loss, x_hat = model(img)
        recon_loss = nn.MSELoss()(x_hat, img)
        loss = recon_loss + embedding_loss
        test_loss += loss.item()
    
    # エポックごとのロスを計算し、表示
    train_loss /= len(trainloader.dataset)
    test_loss /= len(testloader.dataset)
    print('epock %d train_loss: %.5f test_loss: %.5f'%(i,train_loss,test_loss))
    train_loss_log.append(train_loss)
    test_loss_log.append(test_loss)

    # 最終エポックでモデルを保存
    if i==(max_epoch):
        torch.save({'param':model.to('cpu').state_dict(),
                    'opt':opt.state_dict(),
                    'epoch': i},
                    'VQVAE_local.pth')

# ロスのプロット
plt.suptitle('Loss')
plt.plot(train_loss_log, label='train_loss')
plt.plot(test_loss_log, label='test_loss')
plt.grid(axis='y')
plt.legend()
plt.show()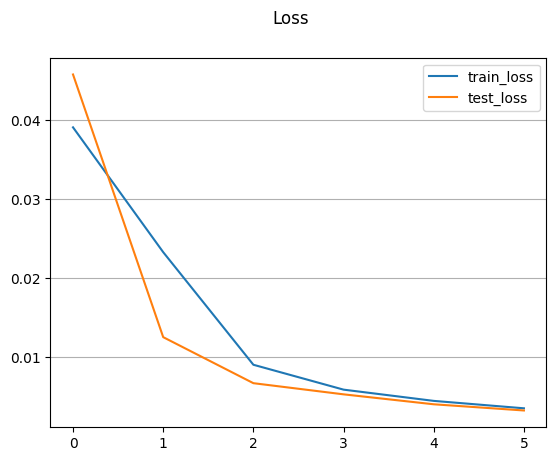

訓練済みのVQ-VAEモデルをロードし、テストセットから1つの画像を取得して、その画像の元のバージョンとモデルによって再構築されたバージョンを表示します。

import random  # ランダムな整数を生成するためのライブラリのインポート

# 保存されたモデルのファイルパス
model_path = "VQVAE_local.pth"
# VQVAEモデルのインスタンスの作成
model = VQVAE(128, 32, 2, 512, 64, .25)
# 保存されたモデルのパラメータをロード
checkpoint = torch.load(model_path)
model.load_state_dict(checkpoint['param'])
# モデルを適切なデバイス（GPUまたはCPU）に移動
model = model.to(device)
# テストデータローダーから最初のバッチを取得し、適切なデバイスに移動
img_batch = next(iter(testloader))[0].to(device)

# バッチからランダムにインデックスを選ぶ
random_index = random.randint(0, img_batch.size(0) - 1)

# 選ばれた画像をバッチに変換（次元を追加）
img = img_batch[random_index].unsqueeze(0)
# モデルを通じて画像をエンコードし、デコード
embedding_loss, x_hat = model(img)
# 出力画像をCPUに移動し、NumPy配列に変換
pred = x_hat[0].to('cpu').detach().numpy().reshape(28, 28, 1)
# 元の画像をCPUに移動し、NumPy配列に変換
origin = img[0].to('cpu').detach().numpy().reshape(28, 28, 1)

# 元の画像を表示
plt.subplot(211)
plt.imshow(origin, cmap="gray")
plt.xticks([])  # x軸の目盛りを非表示
plt.yticks([])  # y軸の目盛りを非表示
plt.text(x=3, y=2, s="original image", c="red")  # テキストラベルの追加

# 出力画像を表示
plt.subplot(212)
plt.imshow(pred, cmap="gray")
plt.text(x=3, y=2, s="output image", c="red")  # テキストラベルの追加
plt.xticks([])  # x軸の目盛りを非表示
plt.yticks([])  # y軸の目盛りを非表示
plt.show()  # グラフの表示

元の画像と再構築された画像を並べて表示します。これにより、モデルがどれだけうまく画像を再構築できたかを視覚的に評価できます。

まとめ

最後までご覧いただきありがとうございました。

カテゴリー: E資格、資格

タグ: E資格