このシリーズではE資格対策として、シラバスの内容を項目別にまとめています。

E資格まとめ

試験概要 ディープラーニングの理論を理解し、適切な手法を選択して実装する能力や知識を有しているかを認定する。 １．応用数学 （１）確率・統計 （２）情報理論 ２．機…

つくもちブログ　〜Python&AIまとめ〜
目次

確率的勾配降下法

概要

機械学習では、特定のタスク（例えば、画像の分類やテキストの生成など）を最もよくこなすための「最適なモデル」を見つけることが目的です。この「最適なモデル」を見つけるためには、モデルのパラメータ（設定値）を調整することで、何らかの「コスト（損失）関数」を最小化（または最大化）することが求められます。

具体的には、モデルが予測を行う際に、実際の値とどれだけズレがあるかを計算し、そのズレが最小になるようにモデルのパラメータを調整します。このズレが「コスト（損失）」となります。

そして、このコストを最小化するための方法の一つが「勾配降下法」です。ここでいう「勾配」は、コスト関数の傾きを意味します。つまり、勾配降下法では、コストが最も急速に減少する方向（つまり、勾配が最も急な方向）へとモデルのパラメータを徐々に調整していきます。

しかし、全てのデータを一度に用いて勾配を計算すると、データが大量にある場合には計算コストが非常に高くなります。そこで、「確率的勾配降下法」が用いられます。

確率的勾配降下法（SGD）では、全てのデータの代わりに、ランダムに選択した一部のデータ（一つまたは小さなグループ）だけを用いて勾配を計算します。これにより、計算コストを大幅に削減しながら、全体としてはコスト関数を最小化する方向へとモデルのパラメータを調整することが可能となります。

ただし、一部のデータだけを用いるため、パラメータの調整は全体の最適解へと直線的に進むわけではなく、むしろランダムに跳ね回るように進んでいきます。しかし、長い時間を経ると、全体としては最適な方向へと進んでいくことになります。

式

SGDの数学的な説明を以下に示します。まず、損失関数 L(θ) が与えられます。ここで、θ は学習するパラメータです。確率的勾配降下法の更新式は以下のようになります。

$$ \theta_{\text{new}} = \theta_{\text{old}} – \eta \nabla L(\theta_{\text{old}}) $$
\begin{align*} \theta_{\text{new}} & : \text{新しいパラメータの値} \\ \theta_{\text{old}} & : \text{古いパラメータの値} \\ \eta & : \text{学習率（ステップサイズ）} \\ \nabla L(\theta_{\text{old}}) & : \text{損失関数の勾配} \end{align*}

確率的勾配降下法の長所

  1. 計算効率: 一度の更新に一つのデータ点しか使用しないため、計算効率が非常に高いです。
  2. 大規模データ対応: データセットが大きくても、一度に一つのデータ点を処理するため、メモリ効率が良いです。
  3. 局所最適解の回避: ランダムにデータ点を選ぶため、局所最適解に囚われにくい場合があります。
  4. オンライン学習: 新しいデータが逐次的に来る状況でも、SGDを用いて継続的に学習することが可能です。

確率的勾配降下法の長所

  1. 収束の不安定性: ランダムにデータ点を選ぶため、収束が不安定になることがあるため、適切な学習率の選定が重要です。
  2. ハイパーパラメータ調整: 学習率などのハイパーパラメータの調整が難しいことがあるので、実践的な利用には経験が必要です。
  3. 非効率な探索: 一つずつデータを用いるため、方向の選定がランダムになることが多く、最適解に辿り着くのが遅いことがある。

確率的勾配降下法の実装

class SGD:

    def __init__(self, lr=0.01):
        self.lr = lr
        
    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]

このクラスは、SGDの基本的なメカニズムを表しています。初期化関数 __init__ で学習率（learning rate）を設定します。学習率は、パラメータの更新量を制御する重要な要素で、通常は0.01や0.001などの小さな値が設定されます。

次に update 関数を見てみましょう。この関数は、モデルのパラメータを更新するために使用されます。具体的には、各パラメータに対して勾配（コスト関数の微分値）を計算し、その勾配に学習率を掛けた値をパラメータから引きます。これにより、コスト関数が最小となる方向へパラメータが更新されます。

ここでの params はモデルのパラメータ（例えば、ニューラルネットワークの重みやバイアスなど）を表し、 grads はそれらのパラメータに対する勾配（コスト関数の微分値）を表します。つまり、各パラメータは params[key] -= self.lr * grads[key] という行によって更新されます。

このコードの特徴として、SGDでは全体としてコスト関数を最小化する方向へとパラメータが更新されるのではなく、一度に一つ（または一部）のデータだけを用いてパラメータが更新されるため、一見するとランダムに跳ね回るように見える点があります。しかし、全体としては最適な方向へと進んでいくことになります。

SGDによる最適化の更新経路

SGDによる最適化の更新経路

SGDを実装し、与えられた関数の最小値を探します。

# 必要なモジュールをインポート
import numpy as np
import matplotlib.pyplot as plt

# SGD (Stochastic Gradient Descent) クラスを定義します。
# このクラスは最適化手法の一つである確率的勾配降下法を実装します。
class SGD:

    # コンストラクタで学習率を設定します。
    def __init__(self, lr=0.01):
        self.lr = lr
    
    # パラメータを更新するメソッドです。
    # 勾配（grads）に学習率（lr）を掛けた値を元のパラメータから引くことで、パラメータを更新します。
    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]

# 2変数関数を定義します。この関数の最小値をSGDを使って求めます。
def function_2(x):
    return (1/20)*x[0]**2 + x[1]**2

# 数値的に勾配を求める関数を定義します。
def numerical_gradient(f, x):
    h = 1e-4  # 微小な変化量
    grad = np.zeros_like(x)  # 勾配を保存するための配列を準備
    
    # 各パラメータごとに勾配を計算
    for idx in range(x.size):
        tmp_val = x[idx]
        
        # f(x+h)の計算
        x[idx] = tmp_val + h
        fxh1 = f(x)
        
        # f(x-h)の計算
        x[idx] = tmp_val - h
        fxh2 = f(x)
        
        # 勾配の計算
        grad[idx] = (fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val
    
    return grad  # 勾配を返す

# 初期パラメータを設定
init_params = {'x': np.array([-7.0, 2.0])}

# SGDのインスタンスを作成
optimizer = SGD(lr=0.95)

# 結果を格納するリスト
path = [init_params['x'].copy()]

# 100回のループでパラメータを更新
for i in range(100):
    grads = {'x': numerical_gradient(function_2, init_params['x'])}  # 勾配を計算
    optimizer.update(init_params, grads)  # パラメータを更新
    path.append(init_params['x'].copy())  # 更新したパラメータをリストに追加

# 更新履歴をnumpy arrayに変換
path = np.array(path)

# 結果をプロット
plt.figure(figsize=(6,6))  # グラフのサイズを指定
plt.plot(path[:,0], path[:,1], 'o-', color="blue")  # パラメータの更新履歴をプロット
plt.xlim(-7.5, 7.5)  # x軸の範囲を指定
plt.ylim(-2.5, 2.5)  # y軸の範囲を指定
plt.xlabel("X0")  # x軸のラベルを設定
plt.ylabel("X1")  # y軸のラベルを設定
plt.grid()  # グリッドを表示
plt.show()  # グラフを表示
  1. SGDクラス：SGDオプティマイザーを定義しています。このクラスは学習率（lr）というパラメータを持ち、updateメソッドを使ってパラメータの更新を行います。このupdateメソッドは、各パラメータをその勾配に学習率を掛けた値で更新します。
  2. function_2：最適化する対象の関数を定義しています。この関数は2次元の入力を取り、各成分の2乗の和を計算します。
  3. numerical_gradient：数値的に勾配を計算する関数です。各パラメータに対して、微小な変化を加えて関数の変化を計算し、これを使って勾配を近似します。
  4. 最適化のプロセス：初期パラメータを設定し、SGDオプティマイザーを作成します。次に、100回の更新を行い、各ステップでのパラメータの値を記録します。
  5. 結果の可視化：最適化の過程を2次元のグラフにプロットします。各ステップでのパラメータの値（X0とX1）をプロットし、最適化の過程を可視化します。

このコードの目的は、与えられた関数（function_2）の最小値を勾配降下法（具体的にはSGD）を用いて探すことです。それぞれのステップで、パラメータはその勾配方向に移動し、最終的には関数の最小値に近づくはずです。

SGDと学習率

lrとは学習率（learning rate）のことで、このパラメータは勾配降下法のステップサイズを決定します。つまり、パラメータをどれだけ速く更新するかを決定します。

lr=0.95とlr=0.1では、学習率が大きく異なります。一般的に、学習率が大きい場合（lr=0.95）、パラメータの更新は大きく、学習が速く進みます。しかし、その反面、最適解を”通り過ぎて”しまう可能性があり、収束が不安定になることがあります。

一方で、学習率が小さい場合（lr=0.1）、パラメータの更新は緩やかで、学習はゆっくりと進みます。このため、最適解を見逃すリスクは低くなりますが、収束に時間がかかる可能性があります。また、極小値にトラップされやすくなる可能性もあります。

したがって、適切な学習率を選択することは、最適化の成功にとって重要です。学習率は大きすぎても小さすぎてもならず、適切なバランスを見つける必要があります。学習率を選択する際には、一般的には様々な値を試し、最も良い結果を得る値を選択します。

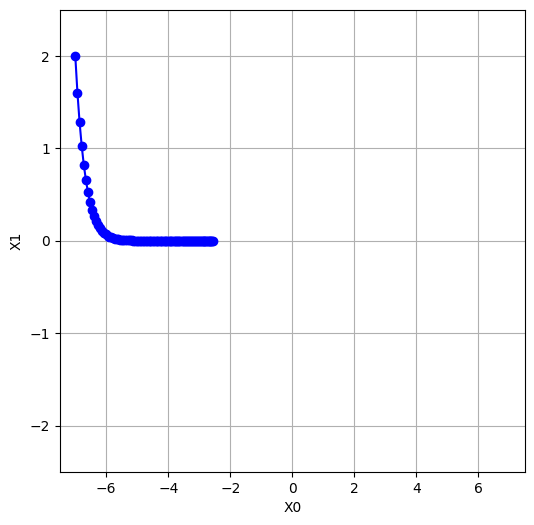
lr=0.1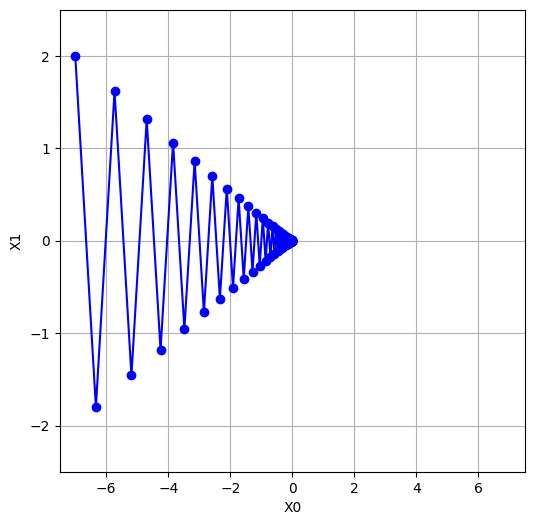
lr=0.95

まとめ

最後までご覧いただきありがとうございました。

カテゴリー
E資格、資格
タグ
前の記事
【E資格まとめ】マルチタスク学習
2023年5月28日
次の記事
【Stable Diffusion】BRA V5で画像生成してみる【画像生成】
2023年5月30日