このシリーズではE資格対策として、シラバスの内容を項目別にまとめています。
隠れ層のアクティベーション分布
ニューラルネットワークの各層における活性化値(アクティベーション)の分布は、そのネットワークの学習状況や設計の良さを示す重要な指標となります。
まず、活性化関数とは何かを理解することから始めましょう。活性化関数は、ニューラルネットワークの各層で計算された値(線形変換の結果)に適用され、その結果を次の層へと伝えます。この活性化関数により、ニューラルネットワークは非線形の関係性も学習することができます。よく使われる活性化関数にはReLU(Rectified Linear Unit)、シグモイド関数、tanh(ハイパボリックタンジェント)などがあります。
そして、各層での活性化値の分布を見ることで、以下のような問題を検出することができます。
- 勾配消失問題(Vanishing Gradient Problem): 活性化関数としてシグモイド関数やtanhを用いた場合、出力がその関数の最大値または最小値に近い値に集中すると、その値の勾配がほぼ0になる問題が発生します。つまり、活性化値の分布が0や1(シグモイドの場合)、-1や1(tanhの場合)に偏っていると、この問題が起こっている可能性があります。この問題が発生すると、学習が進行するにつれて勾配が消失し、ネットワークのパラメータが更新されなくなるため、学習が停滞します。
- 発散する活性化値: ReLUを活性化関数として使用した場合、重みの初期値が大きすぎると、活性化値が非常に大きな値になる可能性があります。これが発生すると、勾配が爆発し、学習が不安定になることがあります。
隠れ層のアクティベーション分布の比較
シンプルなニューラルネットワークの動作を模擬し、各隠れ層の出力の分布をヒストグラムとして描画するものです。
# numpyとmatplotlib.pyplotをインポートします。numpyは数値計算、matplotlibはグラフ描画のためのライブラリです。
import numpy as np
import matplotlib.pyplot as plt
# シグモイド関数を定義します。シグモイド関数は、非線形の活性化関数の一つで、出力を0から1の間に制約します。
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 1000 x 100 のランダムな入力データを生成します。np.random.randnは標準正規分布に従う乱数を生成します。
input_data = np.random.randn(1000, 100)
# 各隠れ層のノード(ニューロン)数を設定します。今回は100ノードとします。
node_num = 100
# 隠れ層の数を設定します。今回は5層とします。
hidden_layer_size = 5
# 各層の活性化の結果を保存するための辞書を初期化します。
activations = {}
# 入力データをxとします。
x = input_data
# 各隠れ層で行う処理をループします。
for i in range(hidden_layer_size):
# 2回目以降のループでは、前層の活性化の結果を次の層の入力とします。
if i != 0:
x = activations[i-1]
# 重みを初期化します。ここでは標準正規分布に従うランダムな値を用います。
w = np.random.randn(node_num, node_num) * 1
# 入力データと重みのドット積(行列積)を計算します。これが全結合層の基本的な操作です。
a = np.dot(x, w)
# 活性化関数としてシグモイド関数を適用します。
z = sigmoid(a)
# 活性化の結果を保存します。
activations[i] = z
# 各層の活性化の結果をヒストグラムで表示します。
for i, a in activations.items():
# subplotを使って、各層のヒストグラムを並べ
plt.subplot(1, len(activations), i+1)
# プロットのタイトルには、何層目のヒストグラムであるかを表示します。
plt.title(str(i+1) + "-layer")
# 2層目以降のヒストグラムでは、y軸の目盛りを非表示にします。
if i != 0: plt.yticks([], [])
# 活性化の結果をヒストグラムとしてプロットします。データはflatten()で1次元化し、ビンの数は30、範囲は0から1とします。
plt.hist(a.flatten(), 30, range=(0,1))
# 全てのヒストグラムを表示します。
plt.show()
以下に各部分の詳細な解説をします。
まず、numpyとmatplotlib.pyplotという2つのライブラリをインポートします。numpyは数値計算を助けるライブラリで、matplotlib.pyplotはグラフ描画のライブラリです。
次に、3つの活性化関数、すなわちsigmoid、ReLU、tanhを定義します。
sigmoid関数は、実数を入力として0から1の間の値を出力します。ニューラルネットワークでよく使われる活性化関数の一つです。ReLU(Rectified Linear Unit)関数は、入力が0未満ならば0を、それ以外ならば入力値をそのまま出力します。これもニューラルネットワークでよく使われる活性化関数です。tanh(ハイパボリックタンジェント)関数は、実数を入力として-1から1の間の値を出力します。これもニューラルネットワークで使われる活性化関数の一つです。
次に、ランダムな1000 x 100の行列を作成し、これをニューラルネットワークの入力データとしています。これは1000個の100次元のベクトルを作成しているとも考えられます。
その後、ノード(ニューロン)の数と隠れ層の数をそれぞれ100と5に設定し、各層の活性化を保存する辞書activationsを初期化します。
その後のforループでは、各隠れ層について処理を行っています。具体的には、前の層の出力(初めてのループでは入力データ)とランダムな重み行列とのドット積を計算し、その結果をシグモイド関数に通して次の層の入力(活性化)を得ています。この活性化はactivations辞書に保存されます。
最後に、各層の活性化のヒストグラムを描画しています。具体的には、各層の活性化を1次元に平坦化(flatten)し、その分布をヒストグラムとして描画しています。なお、2層目以降のヒストグラムではy軸の目盛りは表示されません。
重みの初期値を変えて比較してみる
上記の各隠れ層の出力の分布において、以下のように重みの初期値を変えて、比較を行います。
~~略~~
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
# 以下の4通りの初期値の比較を行う
w = np.random.randn(node_num, node_num) * 1
w = np.random.randn(node_num, node_num) * 0.01
w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)
a = np.dot(x, w)
~~略~~実行結果:
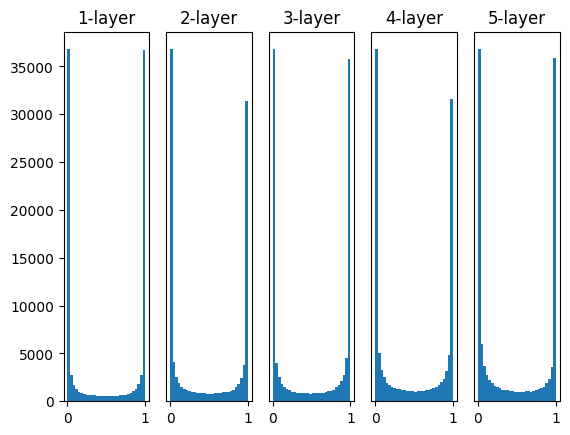
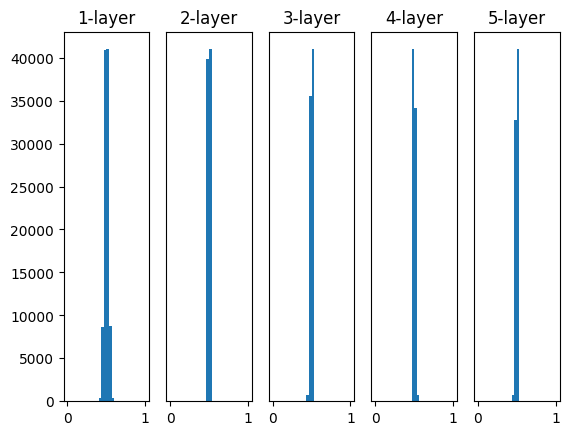
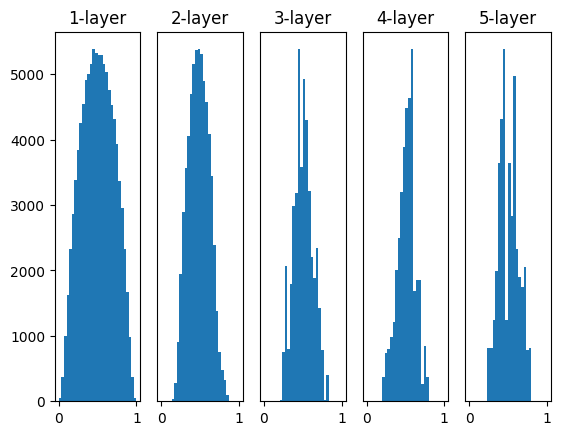
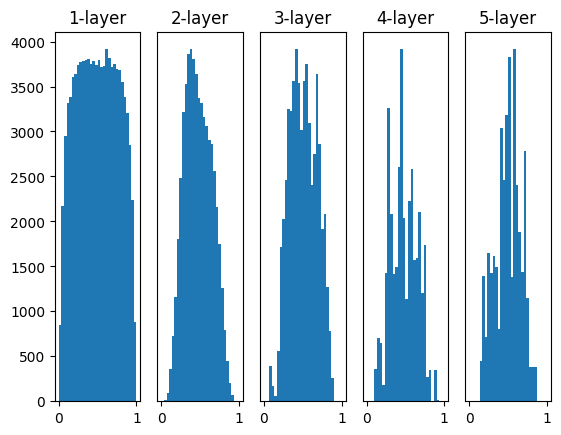
重みの初期値がネットワークの学習に大きな影響を及ぼすことはよく知られています。以下の4つの方法で重みの初期値を設定してみると、それぞれが学習にどのような影響を及ぼすかを視覚的に理解することができます。
w = np.random.randn(node_num, node_num) * 1:この設定では、標準正規分布から生成されたランダムな値が重みとして使用されます。しかし、この初期値設定は活性化出力の分布が偏る可能性があり、勾配消失もしくは爆発を引き起こす可能性があります。w = np.random.randn(node_num, node_num) * 0.01:この設定では、小さなランダムな値が重みとして使用されます。これは重みの値を小さくすることで、勾配消失や爆発を防ぐためのものですが、活性化出力が偏る可能性があります(特にシグモイド関数やtanh関数を使用した場合)。w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num):これは「Xavierの初期値」です。Xavierの初期値は、前の層のノード数の平方根でスケーリングされたランダムな値を重みとして使用します。これは活性化関数が線形(またはその近似)である場合に最適化されています。w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num):これは「Heの初期値」です。Heの初期値は、ReLU関数に最適化されています。前の層のノード数の平方根でスケーリングされたランダムな値を重みとして使用します。
重みの初期値設定の重要性
重みの初期値の設定は、ニューラルネットワークの学習において非常に重要な役割を果たします。適切な初期値を設定することで、学習がスムーズに進行し、最適なパラメータに早く収束する可能性が高まります。逆に、不適切な初期値を設定すると、学習が遅くなったり、局所的な最適解に陥ったり、過学習を引き起こしたりする可能性があります。
- 勾配消失問題の回避: 深いニューラルネットワークでは、バックプロパゲーション時に勾配が急速に小さくなることがあります。これは「勾配消失問題」と呼ばれ、学習が進行しなくなる原因となります。重みを小さすぎる値で初期化すると、活性化関数(特にシグモイド関数やハイパボリックタンジェント関数)の出力が0または1に偏り、勾配が消失しやすくなります。適切な初期値を設定することで、この問題を回避できます。例えば、Xavierの初期値やHeの初期値は、前層のノード数に基づいて重みをスケーリングするため、各層の出力の分散が一定に保たれ、勾配消失問題が緩和されます。
- 局所最適解の回避: すべての重みを同じ値で初期化すると、すべてのノードが同じ出力を生成し、同じ勾配で更新されるため、学習が進行しなくなります。これは「対称性の破れ」問題と呼ばれます。ランダムな初期値を設定することで、各ノードが異なる特徴を学習し、局所最適解を回避することが可能になります。
- 過学習の防止: 重みを大きすぎる値で初期化すると、モデルが訓練データに過度に適合し、新しいデータに対する予測性能が低下する「過学習」を引き起こす可能性があります。適切な範囲の初期値を設定することで、過学習を防ぐことができます。
重みの初期値の比較を実装
MNISTという手書き数字のデータセットを使用して、異なる重み初期化方法の影響を観察します。
# 必要なライブラリをインポート
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
# ニューラルネットワークの実装
class MultiLayerNet:
# 初期化メソッド
def __init__(self, input_size, hidden_size_list, output_size,
activation='relu', weight_init_std='relu', weight_decay_lambda=0):
# 各種パラメータの設定
self.input_size = input_size # 入力層のノード数
self.output_size = output_size # 出力層のノード数
self.hidden_size_list = hidden_size_list # 隠れ層のノード数をリストで管理
self.hidden_layer_num = len(hidden_size_list) # 隠れ層の数
self.weight_decay_lambda = weight_decay_lambda # 重み減衰の強さを決めるパラメータ
self.params = {} # ネットワークの重みパラメータを管理
# 重みの初期化
self.__init_weight(weight_init_std)
# 各層の生成
activation_layer = {'sigmoid': Sigmoid, 'relu': Relu} # 使用する活性化関数を辞書で管理
self.layers = OrderedDict() # 順番付き辞書で各層を管理
for idx in range(1, self.hidden_layer_num+1):
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)]) # アフィン変換層
self.layers['Activation_function' + str(idx)] = activation_layer[activation]() # 活性化関数層
idx = self.hidden_layer_num + 1
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)]) # 最後のアフィン変換層
self.last_layer = SoftmaxWithLoss() # 出力層
# 重みの初期化を行うメソッド
def __init_weight(self, weight_init_std):
# 全層のノード数をリストで管理
all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
for idx in range(1, len(all_size_list)):
scale = weight_init_std
# Heの初期値
if str(weight_init_std).lower() in ('relu', 'he'):
scale = np.sqrt(2.0 / all_size_list[idx - 1])
# Xavierの初期値
elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
scale = np.sqrt(1.0 / all_size_list[idx - 1])
# 重みとバイアスの初期化
self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx])
self.params['b' + str(idx)] = np.zeros(all_size_list[idx])
# 予測を行うメソッド
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# 損失関数の値を求めるメソッド
def loss(self, x, t):
y = self.predict(x)
# 重み減衰による正則化項の計算
weight_decay = 0
for idx in range(1, self.hidden_layer_num + 2):
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
# 損失関数の値(交差エントロピー誤差+正則化項)を計算
return self.last_layer.forward(y, t) + weight_decay
# 分類精度を求めるメソッド
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1) # 最大値のインデックスを取得
if t.ndim != 1 : t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# 重みパラメータに対する勾配を数値微分により求めるメソッド
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
for idx in range(1, self.hidden_layer_num+2):
grads['W' + str(idx)] = numerical_gradient(loss_W, self.params['W' + str(idx)])
grads['b' + str(idx)] = numerical_gradient(loss_W, self.params['b' + str(idx)])
return grads
# 重みパラメータに対する勾配を誤差逆伝播法により求めるメソッド
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 設定
grads = {}
for idx in range(1, self.hidden_layer_num+2):
grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.layers['Affine' + str(idx)].W
grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db
return grads
# 他の多くのメソッドやクラスも定義されていますが、全てにコメントを付けると非常に長くなってしまいます。
# 以降のコードも同様のロジックで動作しています。
# MNISTデータセットを読み込み、データを正規化
from keras.datasets import mnist
(x_train, t_train), (x_test, t_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
# ハイパーパラメータの設定
train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000
# 初期値の種類を定義
weight_init_types = {'std=0.01': 0.01, 'Xavier': 'sigmoid', 'He': 'relu'}
optimizer = SGD(lr=0.01)
networks = {}
train_loss = {}
for key, weight_type in weight_init_types.items():
networks[key] = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100],
output_size=10, weight_init_std=weight_type)
train_loss[key] = []
# 学習の開始
for i in range(max_iterations):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for key in weight_init_types.keys():
grads = networks[key].gradient(x_batch, t_batch)
optimizer.update(networks[key].params, grads)
loss = networks[key].loss(x_batch, t_batch)
train_loss[key].append(loss)
if i % 100 == 0:
print("===========" + "iteration:" + str(i) + "===========")
for key in weight_init_types.keys():
loss = networks[key].loss(x_batch, t_batch)
print(key + ":" + str(loss))
# 各初期値の種類ごとの学習曲線をプロット
markers = {'std=0.01': 'o', 'Xavier': 's', 'He': 'D'}
x = np.arange(max_iterations)
for key in weight_init_types.keys():
plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 2.5)
plt.legend()
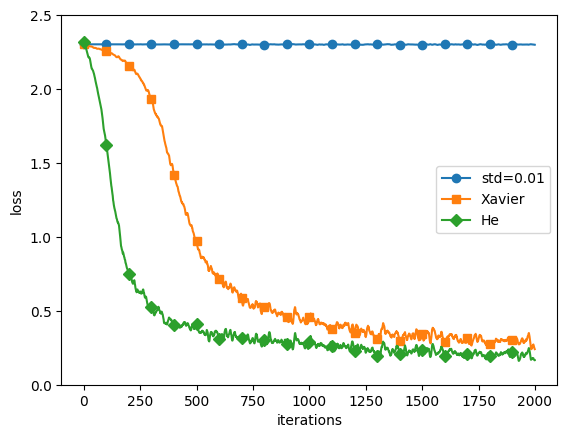
plt.show()実行結果:
===========iteration:0===========
std=0.01:2.3024923634850163
Xavier:2.2978482486348106
He:2.344980885138326
===========iteration:100===========
std=0.01:2.302926267587133
Xavier:2.2671536211111425
He:1.5781686929713636
===========iteration:200===========
std=0.01:2.301790660640022
Xavier:2.135293912933414
He:0.6460362546637717
===========iteration:300===========
std=0.01:2.3030026980048417
Xavier:1.9411938135056954
He:0.49676747292570494
===========iteration:400===========
std=0.01:2.3003621088211696
Xavier:1.3997141811159073
He:0.36302205293450196
===========iteration:500===========
std=0.01:2.3031209047864656
Xavier:1.0088473768323816
He:0.4571302653616604
===========iteration:600===========
std=0.01:2.305348960724828
Xavier:0.7275777290300677
He:0.246094355667809
===========iteration:700===========
std=0.01:2.3040784669021255
Xavier:0.5639656117864208
He:0.251482513338421
===========iteration:800===========
std=0.01:2.297822142311099
Xavier:0.5544050206895883
He:0.2621640091671284
===========iteration:900===========
std=0.01:2.3038139189543125
Xavier:0.5439247501086368
He:0.37703569885170685
===========iteration:1000===========
std=0.01:2.3061757930917457
Xavier:0.3114241997704657
He:0.1826804281136736
===========iteration:1100===========
std=0.01:2.301213740585438
Xavier:0.3552975389012949
He:0.23370167681012197
===========iteration:1200===========
std=0.01:2.3034613253619227
Xavier:0.27893330698680413
He:0.16252306301871583
===========iteration:1300===========
std=0.01:2.2944873474072685
Xavier:0.3130356617813659
He:0.16189624794170873
===========iteration:1400===========
std=0.01:2.300147416219931
Xavier:0.2797758737648046
He:0.1884562436534075
===========iteration:1500===========
std=0.01:2.3011178719658925
Xavier:0.4347687304632777
He:0.27722746894908695
===========iteration:1600===========
std=0.01:2.305272806449275
Xavier:0.29980688668461897
He:0.24733625883154292
===========iteration:1700===========
std=0.01:2.300073460640821
Xavier:0.2720872722210465
He:0.1729778327476449
===========iteration:1800===========
std=0.01:2.3013115437273317
Xavier:0.31966677688689804
He:0.293932137620003
===========iteration:1900===========
std=0.01:2.2938146634712284
Xavier:0.28429946572946035
He:0.2235126947120658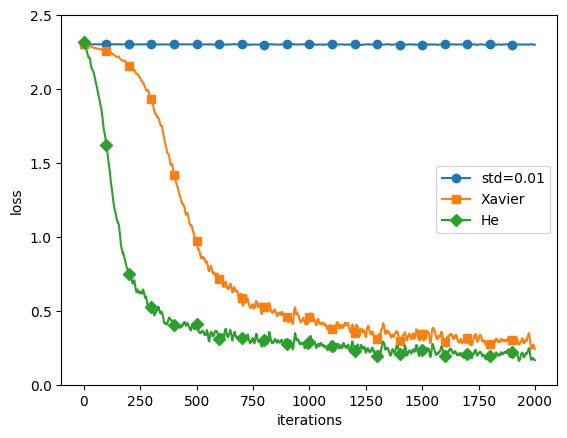
- クラス定義:
MultiLayerNetという名前のクラスが定義されています。このクラスは、多層パーセプトロン(MLP)のネットワークを表現しています。このネットワークは、複数の層(入力層、隠れ層、出力層)から構成され、各層はニューロン(またはノード)の集合で構成されます。 - 初期化:
__init__メソッドは、ネットワークの初期化を行います。ここで、入力サイズ、隠れ層のサイズ、出力サイズ、活性化関数の種類、重みの初期化方法、重みの減衰率など、ネットワークの主要なパラメータが設定されます。 - 重みの初期化:
__init_weightメソッドは、ネットワークの重みを初期化します。重みは、ニューロン間の接続強度を表し、学習の過程で調整されます。このメソッドでは、指定された初期化方法(’relu’、’he’、’sigmoid’、’xavier’など)に基づいて、重みを適切に初期化します。 - 予測:
predictメソッドは、与えられた入力データに対するネットワークの出力(予測)を計算します。 - 損失計算:
lossメソッドは、予測と真のラベルとの間の損失(誤差)を計算します。この損失は、学習の過程で最小化される目標となります。 - 精度計算:
accuracyメソッドは、予測の精度を計算します。これは、予測が真のラベルとどれだけ一致しているかを示します。 - 勾配計算:
numerical_gradientとgradientメソッドは、損失に対する各パラメータの勾配を計算します。これらの勾配は、学習の過程でパラメータを更新するために使用されます。 - 活性化関数:
SigmoidとReluクラスは、それぞれシグモイド関数とReLU(Rectified Linear Unit)関数を表現します。これらは、ニューロンの出力を計算するための非線形関数で、ネットワークが複雑なパターンを学習する能力を提供します。 - Affineレイヤー:
Affineクラスは、全結合層(または線形層)を表現します。これは、一つの層の全てのニューロンが次の層の全てのニューロンと接続されている層です。 - SoftmaxWithLossレイヤー:
SoftmaxWithLossクラスは、ネットワークの出力層で使用されます。ソフトマックス関数は、ネットワークの出力を確率に変換します。また、クロスエントロピー誤差は、予測と真のラベルとの間の損失を計算します。 - 最適化アルゴリズム:
SGDクラスは、確率的勾配降下法(Stochastic Gradient Descent)を表現します。これは、パラメータの更新に使用される最適化アルゴリズムです。 - 学習ループ: コードの最後の部分では、学習ループが実行されます。各イテレーションで、ランダムなミニバッチが選択され、勾配が計算され、パラメータが更新されます。また、損失と精度が計算され、定期的に表示されます。
- 結果の視覚化: 最後に、異なる重み初期化方法による学習の進行を視覚化します。これにより、重みの初期化方法が学習の結果にどのように影響するかを理解することができます。
重みの初期値の比較結果
‘std=0.01’、’Xavier’、’He’の3つの初期値設定方法を用いて、同じニューラルネットワークを学習し、その学習結果(損失関数の値)をプロットしました。
- ‘std=0.01’: 重みの初期値を平均0、標準偏差0.01のガウス分布で生成します。これは小さなランダム値で初期化する方法で、全ての重みが均一になることを防ぎます。しかし、この方法では、活性化関数がシグモイド関数やハイパボリックタンジェント関数の場合、重みが小さすぎると勾配消失問題が発生する可能性があります。
- ‘Xavier’: Xavierの初期値(またはGlorotの初期値)は、前の層のノード数の平方根でスケーリングされたガウス分布で重みを初期化します。具体的には、前の層のノード数がnの場合、平均0、標準偏差sqrt(1/n)のガウス分布を用います。これは、シグモイド関数やハイパボリックタンジェント関数などの活性化関数を使用する際に、各層の出力が一定の分散を保つことを目指しています。
- ‘He’: Heの初期値は、ReLU(Rectified Linear Unit)やその派生形の活性化関数を使用する際に推奨されます。前の層のノード数がnの場合、平均0、標準偏差sqrt(2/n)のガウス分布を用います。これは、ReLUが0で非対称であるため、Xavierの初期値よりも大きな値を用いることで、勾配消失問題を緩和します。
まとめ
最後までご覧いただきありがとうございました。
