このシリーズではE資格対策として、書籍「ゼロから作るDeep Learning」を参考に学習に役立つ情報をまとめています。

<参考書籍>

目次

微分の基本的な概念

微分とは

微分とは、関数y = f(x)のある点xにおける「極限」の概念を用いた変化率です。この極限は、xの微小な変化Δxが0に近づくときの、yの変化Δyとxの変化Δxの比率を表します。微分は、以下のような記号で表されることが多いです。

$$f'(x) = dy/dx$$

ここで、f'(x)は関数f(x)の導関数と呼ばれ、dy/dxはyの変化に対するxの変化の比率を示しています。微分の意味は、ある点xにおいて、関数f(x)がどれくらい急速に増加または減少しているかを示すことができます。具体的には、点xにおける接線の傾きを表しています。接線の傾きが正であれば、関数は増加傾向にあり、傾きが負であれば減少傾向にあります。

機械学習と微分の関係

  1. 最適化問題の解決: 機械学習の多くのアルゴリズムは、最適化問題を解くことでモデルを学習します。例えば、線形回帰やニューラルネットワークでは、損失関数（誤差）を最小化するようなパラメータを見つけることが目標です。この最適化問題を解くために、勾配降下法や確率的勾配降下法などの最適化アルゴリズムが用いられます。これらのアルゴリズムは、損失関数の微分（勾配）を計算し、その情報を使ってパラメータを更新していきます。微分は、損失関数が減少する方向を示すため、最適化アルゴリズムの中核を担っています。
  2. パラメータ更新: 機械学習モデルは、多くの場合、学習過程でパラメータを更新していきます。パラメータの更新は、損失関数に対するパラメータの勾配（微分）に基づいて行われます。勾配は、関数の変化率を示すため、パラメータをどの程度、どの方向に更新すべきかを決定するのに役立ちます。
  3. 正則化手法: 機械学習モデルの過学習を防ぐために、正則化手法がしばしば用いられます。正則化手法は、モデルの複雑さにペナルティを課すことで、汎化性能を向上させることを目指しています。例えば、L1正則化やL2正則化では、パラメータの絶対値や二乗和にペナルティを課します。このような正則化項は、損失関数に含まれ、微分を通じてパラメータ更新に影響を与えます。

極限

極限は、ある関数が特定の点においてどのように振る舞うかを調べるための数学的な概念です。関数f(x)がxがある点aに近づくとき、その極限は以下のように表されます。

$$\lim_{\substack{x\to a\\}}f(x) = L$$

ここで、Lは極限の値です。この式は、「xがaに近づくと、f(x)はLに近づく」と解釈できます。

極限の計算を実装する

例として、以下の関数を考えましょう。

$$ f(x) = (x^2 – 1) / (x – 1)$$

x = 1のとき、分母が0になるため、この関数は未定義です。しかし、極限を使って、xが1に近づくときの関数の振る舞いを調べることができます。

$$\lim_{\substack{x\to 1\\}}f(x) = \lim_{\substack{x\to 1\\}}(x^2 – 1) / (x – 1) $$

この極限は、以下のようなPythonコードを使って求めることができます。

import sympy as sp

x = sp.Symbol('x')
f_x = (x**2 - 1) / (x - 1)

# 極限を求める
lim_f_x = sp.limit(f_x, x, 1)

# 結果を表示する
print("lim(x→1) f(x) =", lim_f_x)

実行結果:

2

数値微分

前方差分と中心差分

数値微分において、関数の導関数を近似する方法として、中心差分（central difference）と前方差分（forward difference）があります。これらの手法は、関数の変化率を近似するために、関数の値の差を用いるものです。

  1. 前方差分: 前方差分は、ある点xにおける関数の導関数を、xとx+hの関数値の差によって近似します。前方差分の計算式は以下の通りです。
$$f'(x) ≈ (f(x+h) – f(x)) / h$$

前方差分は簡単で直感的な方法ですが、打ち切り誤差が大きくなりやすいという欠点があります。

  1. 中心差分: 中心差分は、ある点xにおける関数の導関数を、x-hとx+hの関数値の差によって近似します。中心差分の計算式は以下の通りです。
$$f'(x) ≈ (f(x+h) – f(x-h)) / (2*h)$$

中心差分は、前方差分に比べて打ち切り誤差が小さいという利点があります。これは、中心差分が関数の変化を対称的に捉えるため、誤差が相殺される効果があるからです。

一般的には、中心差分法が前方差分法よりも精度が高いとされています。ただし、どちらの方法を選択するかは、問題の性質や計算コスト、関数の特徴などに応じて決定することが重要です。例えば、関数が境界条件を持つ場合や計算コストが重要な要素である場合には、前方差分が適切な選択となることがあります。

数値微分と解析的な微分

微分には数値微分と解析的な微分の2つの方法があります。それぞれの意味と違いについて、わかりやすく説明します。

  1. 数値微分:数値微分は、関数の値からその微分を近似的に求める手法です。微小な変化量Δxを使って、以下の式で微分係数を求めます。
$$f'(x) ≈ (f(x + Δx) – f(x)) / Δx$$

Δxは小さな値であるため、数値微分は近似値を求める方法です。この手法は、解析的に微分が困難な関数や実験データを扱う際に便利です。ただし、近似のため誤差が生じることがあり、Δxの選び方によって精度が変わります。

  1. 解析的な微分:解析的な微分は、関数の式を使って微分を厳密に求める手法です。微分法則（積分法則、連鎖法則など）を適用し、関数の導関数（微分した結果の関数）を求めます。例えば、
$$f(x) = x^2 $$

の場合、解析的に微分すると、

$$f'(x) = 2x $$

となります。

解析的な微分は厳密な解を求めるため、誤差が生じません。ただし、関数の式が複雑であったり、解析的に微分が困難な場合は適用できないことがあります。

数値微分の実装

ここでは簡単な式の数値微分を実装します。数値微分は、関数の導関数（微分）を求める近似的な方法です。Pythonで数値微分を実装するには、まず関数を定義し、その後、中心差分法を用いて微分を計算します。中心差分法では、ある点xにおける関数の微分値を、その点の前後に少し離れた2点の関数値の差を使って近似的に求めます。具体的には、以下の手順で実装します。

import numpy as np

# 1. 関数を定義する
def function(x):
    return 0.01 * x**2 + 0.1 * x

# 2. 数値微分を計算する関数を実装する
def numerical_diff(f, x):
    h = 1e-4  # 0.0001
    return (f(x + h) - f(x - h)) / (2 * h)

# 3. 微分を計算する点を指定する
x1 = 5.0
x2 = 10.0

# 4. 結果を出力する
print("f'(5) =", numerical_diff(function, x1))
print("f'(10) =", numerical_diff(function, x2))

接線を描画してみます。

import numpy as np
import matplotlib.pyplot as plt

# 1. 関数を定義する
def function(x):
    return 0.01 * x**2 + 0.1 * x

# 2. 数値微分を計算する関数を実装する
def numerical_diff(f, x):
    h = 1e-4  # 0.0001
    return (f(x + h) - f(x - h)) / (2 * h)

# 3. 接線の関数を定義する
def tangent_line(f, x):
    slope = numerical_diff(f, x)
    intercept = f(x) - slope * x
    return lambda t: slope * t + intercept

# 4. グラフを描画する
x = np.arange(0, 20, 0.1)  # 0から20までの範囲を0.1刻みで生成
y = function(x)

plt.plot(x, y, label="y = 0.01x^2 + 0.1x")

x1 = 5.0
x2 = 10.0

y1_tangent = tangent_line(function, x1)(x)
y2_tangent = tangent_line(function, x2)(x)

plt.plot(x, y1_tangent, linestyle="--", label=f"tangent at x={x1}")
plt.plot(x, y2_tangent, linestyle="--", label=f"tangent at x={x2}")

plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()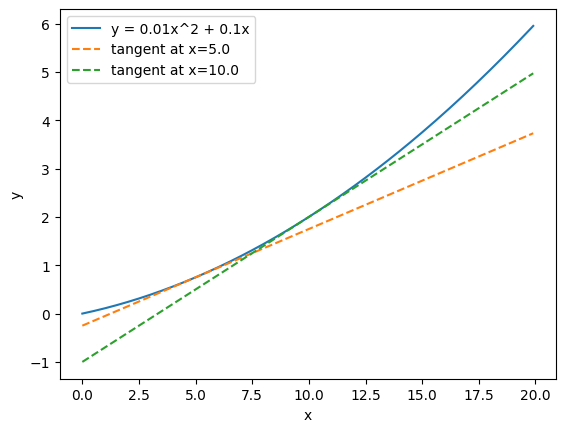

偏微分

偏微分とは、複数の変数を持つ関数において、特定の変数について微分を行う操作です。他の変数は一時的に定数として扱われます。これにより、ある変数が関数に与える局所的な影響を評価することができます。偏微分の記号は通常、∂ を使用して表現されます。例えば、関数 f(x, y) に対して x についての偏微分は ∂f/∂x と表記されます。

まとめ

最後までご覧いただきありがとうございました。

カテゴリー
E資格、資格
タグ
前の記事
【G検定2023まとめ】理解度確認&問題集⑨【直前対策】
2023年3月24日
次の記事
【E資格】第9回:勾配と勾配法【ゼロから作るDeep Learning】
2023年3月26日