【E資格まとめ】活性化関数

このシリーズではE資格対策として、シラバスの内容を項目別にまとめています。

E資格まとめ

試験概要ディープラーニングの理論を理解し、適切な手法を選択して実装する能力や知識を有しているかを認定する。１．応用数学（１）確率・統計（２）情報理論２．機…

つくもちブログ　〜Python&AIまとめ〜

1. シグモイド関数の概要
1.1. シグモイド関数
1.2. シグモイド関数のグラフ
2. Sigmoidレイヤ
2.1. Sigmoidレイヤの実装
3. ソフトマックス関数の概要
3.1. ソフトマックス関数
3.2. ソフトマックス関数の実装
3.3. ソフトマックス関数の計算例
4. ReLU関数の概要
4.1. ReLU関数
4.2. ReLU関数の出力
5. Leaky ReLU関数の概要
5.1. Leaky ReLU関数の出力
6. ハイパボリックタンジェント（tanh）関数
7. まとめ

シグモイド関数の概要

シグモイド関数

シグモイド関数は、「活性化関数」の一つです。この関数の最大の特徴は、入力値がどのようなものであっても、出力値を0から1の範囲に制約するということです。そのため、確率的な解釈が可能であり、二値分類問題の出力層によく使われます。

一般的な式は次のように表されます。

$$
\sigma(x) = \frac{1}{1 + e^{-x}}
$$

シグモイド関数の特徴の一つは、その出力が確率として解釈可能であることです。つまり、分類問題においては、シグモイド関数を活性化関数として使用することで、特定のクラスに属する確率を直接モデリングすることが可能となります。また、シグモイド関数は微分可能であるため、勾配降下法などの最適化アルゴリズムと連携して使用することが可能です。

しかし、他の活性化関数と比較した際に、シグモイド関数にはいくつかの限界があります。一つは「勾配消失問題」です。シグモイド関数の出力が0または1に近づくと、その導関数（勾配）が極めて小さくなります。これは深層学習モデルの学習において、パラメータが適切に更新されなくなるという問題を引き起こします。これを解決するためには、ReLU（Rectified Linear Unit）などの他の活性化関数がしばしば用いられます。

シグモイド関数のグラフ

import matplotlib.pyplot as plt
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.linspace(-10, 10, 100)
y = sigmoid(x)

plt.figure(figsize=(8, 6))
plt.plot(x, y)
plt.title("Sigmoid Function")
plt.xlabel("x")
plt.ylabel("Sigmoid(x)")
plt.grid(True)
plt.show()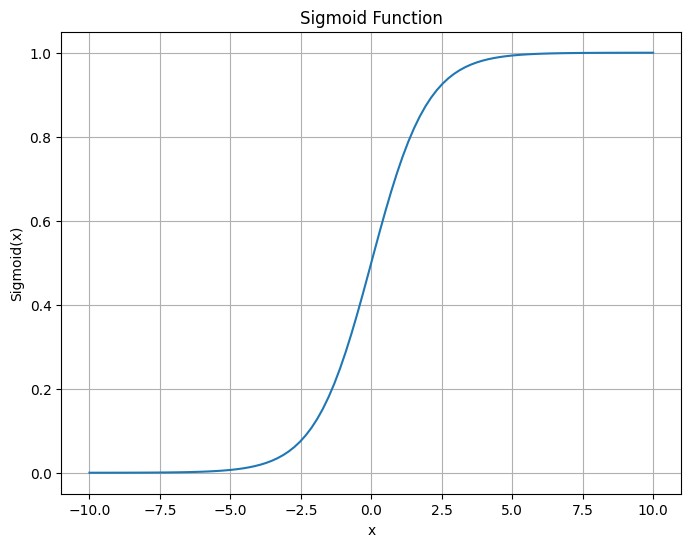

Sigmoidレイヤ

シグモイド活性化関数のクラスを実装しています。シグモイド関数は、ニューラルネットワークの活性化関数として広く使用されていましたが、現在ではReLU関数など他の関数に取って代わられつつあります。シグモイド関数は、入力を0から1の範囲に変換するため、確率に関連する問題で便利です。また、逆伝播も考慮しています。

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

class Sigmoid:
    def __init__(self):
        # out変数を初期化
        self.out = None

    def forward(self, x):
        # シグモイド関数を適用して出力を計算
        out = sigmoid(x)
        # 出力をインスタンス変数に保存
        self.out = out
        # 出力を返す
        return out

    def backward(self, dout):
        # 逆伝播の際の勾配を計算
        dx = dout * (1.0 - self.out) * self.out

        # 勾配を返す
        return dx

Sigmoidレイヤの実装

適当な数値を持つnumpy配列を作成し、Sigmoidクラスのインスタンスを使って順伝播と逆伝播を実行してみます。

# 適当な数値を持つnumpy配列を作成
x = np.array([-1.0, 0.0, 1.0, -0.5, 2.0, 3.0])
print("入力x:", x)

# Sigmoidクラスのインスタンスを作成
sigmoid_layer = Sigmoid()

# 順伝播
out = sigmoid_layer.forward(x)
print("順伝播の結果:", out)

# 逆伝播のための適当な勾配を作成
dout = np.array([1.0, 1.0, 1.0, 1.0, 1.0, 1.0])

# 逆伝播
dx = sigmoid_layer.backward(dout)
print("逆伝播の結果:", dx)

実行結果:

入力x: [-1.   0.   1.  -0.5  2.   3. ]
順伝播の結果: [0.26894142 0.5  0.73105858 0.37754067 0.88079708 0.95257413]
逆伝播の結果: [0.19661193 0.25 0.19661193 0.23500371 0.10499359 0.04517666]

順伝播の結果、シグモイド関数は入力配列の要素を0から1の範囲に変換しています。シグモイド関数は、連続的で微分可能な関数であり、確率に関連する問題で役立ちます。
逆伝播の結果、シグモイド関数の勾配が計算されています。この勾配は、シグモイド関数の導関数である sigmoid(x) * (1 - sigmoid(x)) に基づいています。逆伝播の際、この勾配が前の層に伝搬されます。シグモイド関数の勾配は、0から0.25の範囲になります。これは、シグモイド関数が飽和すると（入力の絶対値が大きくなると）、勾配が小さくなり、勾配消失問題が発生することを示しています。これが、現在ではReLU関数など他の活性化関数に取って代わられつつある理由の1つです。

ソフトマックス関数の概要

ソフトマックス関数

ソフトマックス関数は、多クラス分類問題のニューラルネットワークの出力層において、一般的に用いられる活性化関数です。以下にその定義を示します。

ソフトマックス関数の式は次の通りです：

$$
\sigma(z)_j = \frac{e^{z_j}}{\sum_{k=1}^{K}e^{z_k}}
$$

ソフトマックス関数は以下のような特性を持ちます。

出力は0から1の間の値を取り、その合計は1です。これは、出力を確率として解釈することを可能にします。
入力の中で大きい値は、出力の中でも相対的に大きな値を持つようになります。これは、最も確率が高いクラスを選択する際に役立ちます。
ソフトマックス関数は微分可能であるため、バックプロパゲーションのような勾配ベースの最適化アルゴリズムで使うことができます。

ソフトマックス関数の実装

import numpy as np

def softmax(x):
    # オーバーフロー対策として、最大値を引く
    x = x - np.max(x, axis=-1, keepdims=True)
    # ソフトマックスを計算
    y = np.exp(x) / np.sum(np.exp(x), axis=-1, keepdims=True)
    return y

この関数は、入力 x に対してソフトマックス関数を適用します。x はベクトルでも、または2次元配列でも構いません。2次元配列の場合、各行がそれぞれソフトマックス関数を適用する前のスコアを表すベクトルとして解釈されます。

関数内部では、まず入力 x からその最大値を引くことで、数値のオーバーフロー（指数関数の計算により得られる値が大きすぎて表現できなくなる現象）を防いでいます。その後、各要素の指数関数を計算し、それを全要素の指数関数の和で割ることでソフトマックス関数を計算しています。この関数の出力は、入力と同じ形状の配列で、各要素は対応する入力のソフトマックス値になります。

なお、axis=-1, keepdims=True を指定することで、配列の最後の軸（行方向）に沿って操作を行い、結果の形状が元の配列と同じになるように保っています。これにより、この関数がベクトルだけでなく、2次元配列に対しても正しく動作します。

ソフトマックス関数の計算例

import numpy as np

def softmax(x):
    x = x - np.max(x, axis=-1, keepdims=True)
    y = np.exp(x) / np.sum(np.exp(x), axis=-1, keepdims=True)
    return y

# サンプルデータ
scores = np.array([1.0, 2.0, 3.0, 4.0, 1.0, 2.0, 3.0])
print("入力:", scores)

# ソフトマックス関数の計算
probabilities = softmax(scores)
print("出力:", probabilities)

# 確認：確率の合計が1であること
print("確率の合計:", np.sum(probabilities))

上記のコードでは、7つの異なるクラスのスコアを示す1次元配列をサンプルデータとして用意しています。ソフトマックス関数を適用すると、これらのスコアが0から1の範囲の確率に変換され、その合計が1になることを確認できます。これにより、出力を確率分布として解釈することが可能です。

上記のコードを実行すると、以下のような結果が得られます。

入力: [1. 2. 3. 4. 1. 2. 3.]
出力: [0.02364054 0.06426166 0.1746813  0.474833   0.02364054 0.06426166
 0.1746813 ]
確率の合計: 1.0

この結果から、スコアが高い要素（この場合、4番目の要素）が最も確率が高くなり、それ以外の要素の確率が相対的に小さくなっていることが分かります。また、全ての確率を合計すると1になるため、出力は正確な確率分布を表しています。

ReLU関数の概要

ReLU関数

ReLU関数は以下の式で表されます：

$$
f(x) = \max(0, x)
$$

または

$$
f(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{otherwise} \end{cases}
$$

これは、入力値が0以上の場合はそのままの値を出力し、0以下の場合は0を出力するという単純な関数です。ReLU関数のこの特性が、ニューラルネットワークの訓練を助ける数多くの利点を生み出します。

スパース性: ReLUは負の領域で0を出力するため、ニューラルネットワークにおけるアクティベーションのスパース性（一部のニューロンだけが活性化する現象）を生み出すことができます。これは、ネットワークが自然界のパターンをより効率的に学習するのに役立ちます。
勾配消失問題の緩和: ReLUは正の領域で勾配が1であるため、深いネットワークを訓練する際の勾配消失問題を軽減するのに役立ちます。
計算効率: ReLUはその計算が単純であるため、シグモイド関数や双曲線正接関数などの他の活性化関数に比べて計算が高速です。

ReLUはその性質から、特に深層学習モデルにおける隠れ層の活性化関数として広く利用されています。ただし、ReLUには「死んだニューロン」の問題があります。これは、訓練中にあるニューロンが一度でも0以下の値で活性化すると、その後そのニューロンが再び活性化することがなくなってしまう現象を指します。

この問題を緩和するために、ReLUの改良版であるLeaky ReLUやParametric ReLU、そしてExponential Linear Unit (ELU) などの変種が提案されています。これらの関数は、負の領域でも微小な勾配を持つことで「死んだニューロン」の問題を防ぎつつ、ReLUの主要な利点を維持しています。

ReLU関数の出力

import numpy as np
import matplotlib.pyplot as plt

# ReLU関数
def relu(x):
    return np.maximum(0, x)

# -10から10までの値を生成
x = np.linspace(-10, 10, 1000)

# y値を計算
y = relu(x)

# 図を生成
plt.figure(figsize=(10, 6))
plt.plot(x, y)
plt.title('ReLU function')
plt.xlabel('x')
plt.ylabel('ReLU(x)')
plt.grid(True)
plt.show()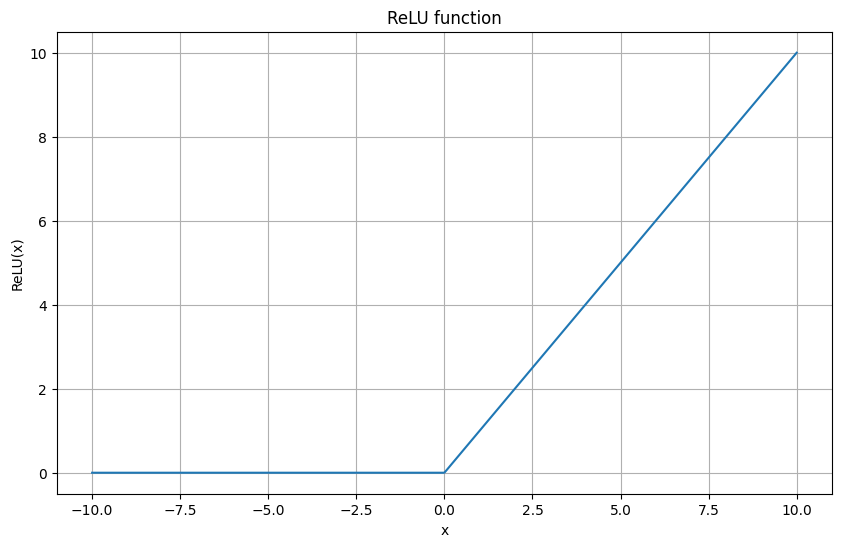

Leaky ReLU関数の概要

Leaky ReLU関数は以下のように定義されます。ここで、xは入力値、aは小さな正の定数（通常は0.01）です。

$$
f(x) = \begin{cases} ax & \text{if } x < 0 \\ x & \text{if } x \geq 0 \end{cases}
$$

この式の意味するところは、もしxが負であれば、その値にaを掛けた値を出力し、もしxが正であれば、そのままの値を出力する、ということです。

ReLU関数の主な問題点の一つに、「死んだニューロン」問題があります。これは、ReLU関数が負の入力に対して0を返すため、学習過程であるニューロンの重みが更新されず、そのニューロンが活性化しなくなる現象を指します。

これに対して、Leaky ReLUでは負の入力に対しても微小な出力をするため、上記の問題をある程度緩和できます。そのため、Leaky ReLUはReLUの代替として、多くの深層学習モデルで使用されています。

Leaky ReLU関数の出力

import numpy as np
import matplotlib.pyplot as plt

def leaky_relu(x, alpha=0.1):
    return np.where(x >= 0, x, alpha * x)

x = np.linspace(-10, 10, 1000)
y = leaky_relu(x)

plt.plot(x, y)
plt.title("Leaky ReLU Activation Function")
plt.xlabel("x")
plt.ylabel("Leaky ReLU(x)")
plt.grid(True)
plt.show()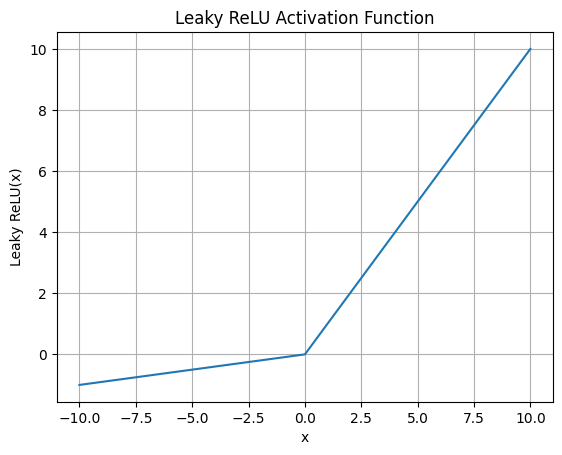

ハイパボリックタンジェント（tanh）関数

ハイパボリックタンジェント関数は-1から1の範囲の値を出力します。そのため、tanh関数は中央の値周辺での勾配が最も急で、その両端では勾配が緩やかになる特徴を持ちます。

$$
f(x) = \tanh(x) = \frac{{e^x – e^{-x}}}{{e^x + e^{-x}}}
$$

tanh関数は、その出力が-1から1の範囲に収束するため、出力の分布が中心化されやすいという利点があります。その結果、学習の収束が早くなる可能性があります。

また、tanh関数はシグモイド関数と比較して、勾配消失問題をやや緩和するとも言われています。これは、tanh関数の出力範囲が-1から1であるため、シグモイド関数の0から1の出力範囲よりも、勾配が0になりにくいからです。

しかしながら、tanh関数もまた勾配消失問題に対しては完全に免疫ではありません。xの絶対値が大きいとき、tanh関数の導関数はほぼ0に近づきます。その結果、多層ネットワークの学習中にバックプロパゲーションが行われると、下層に伝播する勾配が急速に小さくなる可能性があります。これが、いわゆる勾配消失問題です。

この欠点を克服するために、ReLU（Rectified Linear Unit）などの他の活性化関数が提案されています。

import numpy as np
import matplotlib.pyplot as plt

# 入力値の範囲を設定
x = np.linspace(-10, 10, 1000)

# tanh関数を計算
y = np.tanh(x)

# グラフを描画
plt.figure(figsize=(10, 5))
plt.plot(x, y, label="tanh")
plt.title("Graph of the tanh function")
plt.xlabel("x")
plt.ylabel("tanh(x)")
plt.grid(True)
plt.legend()
plt.show()

まとめ

最後までご覧いただきありがとうございました。

カテゴリー: E資格、資格

タグ: E資格