このシリーズではE資格対策として、シラバスの内容を項目別にまとめています。
VAE
オートエンコーダの概要
オートエンコーダとは、非監督学習の一種であり、入力データをエンコーダ部分で低次元に圧縮し(エンコード)、その圧縮された表現をデコーダ部分で元の次元に戻す(デコード)ことを学習します。エンコーダとデコーダは、通常ニューラルネットワークで表現され、入力データとデコーダからの出力(再構成データ)との間の差(再構成誤差)を最小化するように学習します。
再構成誤差を表すための数式は以下のようになります:
VAEの概要
一方、変分オートエンコーダ(VAE)は、オートエンコーダの一種であり、エンコーダ部分がデータの潜在的な表現を確率分布として学習する点で異なります。これにより、デコーダが新たなデータを生成する能力を持つため、生成モデルとしても用いられます。
VAEの学習は、再構成誤差と潜在空間の確率分布が事前分布(通常は標準正規分布)に近づくような誤差(KLダイバージェンス)を最小化するように行われます。これを表す数式は以下のようになります:
具体的には、VAEのエンコーダ部分は入力データから潜在変数の条件付き確率分布を学習します。つまり、入力データ$x$が与えられたときの潜在変数$z$の確率分布Q_{\phi}(Z|X)を学習します。通常、この分布は平均と分散(または標準偏差)の2つのパラメータを持つガウス分布とされます。
一方、デコーダ部分は、潜在変数からデータの生成確率分布$P_{\theta}(X|Z)$を学習します。これは、潜在変数zが与えられたときにデータxをどのように生成するかを学習します。
VAEの目的関数は、以下の2つの部分から成り立ちます:
- 再構成誤差: 入力データxとその再構成x’との間の差を表す。再構成x’は、エンコーダから得られた潜在変数の分布からサンプリングしたzをデコーダに入力して得られます。
- KLダイバージェンス: エンコーダから学習された確率分布Q_{\phi}(Z|X)と、事前に定められた確率分布P(Z)(通常は標準正規分布)との間の距離を表す。この項により、学習された潜在空間が整然とした形状(通常は多変量正規分布)を保つように制約されます。
VAEの特徴
変分オートエンコーダ(VAE)のメリットとデメリットは以下のようにまとめることができます。
メリット:
- 生成能力:VAEは、学習したデータの特性を持つ新たなデータを生成する能力を持っています。これは、例えば、画像生成やテキスト生成など、多くの応用が可能であることを意味します。
- 連続的な潜在空間:VAEは潜在変数の確率分布を学習するため、潜在空間が滑らかで連続的な性質を持ちます。これにより、潜在変数を少しずつ変化させていくと、生成されるデータも連続的に変化します。
- データの圧縮:VAEはデータの高次元表現を低次元の潜在空間に圧縮するため、データの圧縮や次元削減としても使用できます。
デメリット:
- 再構成のぼやけ:VAEが生成するデータはしばしばぼやけた感じになりがちです。これは、デコーダがデータの生成確率分布を学習するため、一部の確率的なノイズが再構成に影響を与えるからです。
- 学習の難易度:再構成誤差とKLダイバージェンスのバランスを取ることが難しく、これにより学習が難しくなることがあります。
- 潜在空間の利用:全ての潜在空間がデータ生成に有効に利用されるわけではなく、一部の空間は無活性となる場合があります。
- 計算負荷:サンプリング操作とバックプロパゲーションの間にある確率的な勾配(reparameterization trick)を必要とするため、計算負荷が高い場合があります。
VAEの活用事例
変分オートエンコーダ(VAE)はその生成能力とデータ圧縮能力から、様々な応用が可能です。以下にいくつかの具体的な実用例を示します。
- 画像生成:VAEは学習した画像データから新たな画像を生成する能力を持ちます。これは、手書きの数字、顔、アニメキャラクターなど、様々な種類の画像生成に応用可能です。
- アノマリー検出:VAEは正常なデータの分布を学習し、その分布から大きく外れたデータ(アノマリー)を検出するために使用することができます。これは、異常検出問題に応用可能です。
- レコメンデーション:ユーザーの行動データを潜在空間にマッピングし、その潜在表現からユーザーが関心を持ちそうなアイテムを生成することで、レコメンデーションシステムに応用することが可能です。
- 画像の超解像:低解像度の画像を入力として、その画像の高解像度バージョンを生成するためにVAEを使用することができます。
- 描画スタイルの転送:ある画像の描画スタイルを捉え、それを別の画像に適用するためにVAEを使用することが可能です。
VAEの実装
変分オートエンコーダ(VAE)を使用して、MNISTデータセット上での教師なし学習を実行します。VAEは、データの生成モデルとして使用されることが多い深層学習の手法で、データの潜在的な構造を捉えることができます。
%matplotlib inline
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
from torchvision import datasets, transforms
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# MNISTデータセットのロード
train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transforms.ToTensor())
test_dataset = datasets.MNIST(root='./data', train=False, transform=transforms.ToTensor())
# 画像データを784次元のベクトルに変換し、正規化
X_train = train_dataset.data.reshape(-1, 784).float() / 255
y_train = F.one_hot(train_dataset.targets, 10).float()
X_test = test_dataset.data.reshape(-1, 784).float() / 255
y_test = F.one_hot(test_dataset.targets, 10).float()
# ハイパーパラメータの定義
batch_size = 100
original_dim = 784
latent_dim = 2
intermediate_dim = 256
epochs = 10
# DataLoaderの作成
train_loader = DataLoader(TensorDataset(X_train, y_train), batch_size=batch_size, shuffle=True)
test_loader = DataLoader(TensorDataset(X_test, y_test), batch_size=batch_size, shuffle=False)
# VAEの定義
class VAE(nn.Module):
def __init__(self):
super(VAE, self).__init__()
# エンコーダ部分の定義
self.encoder_h = nn.Linear(original_dim, intermediate_dim)
self.z_mean = nn.Linear(intermediate_dim, latent_dim)
self.z_sigma = nn.Linear(intermediate_dim, latent_dim)
# デコーダ部分の定義
self.decoder_h = nn.Linear(latent_dim, intermediate_dim)
self.decoder_mean = nn.Linear(intermediate_dim, original_dim)
def encode(self, x):
# エンコーダのフォワードパス
h = F.relu(self.encoder_h(x))
return self.z_mean(h), self.z_sigma(h)
def reparameterize(self, mu, logvar):
# 潜在変数のサンプリング
std = torch.exp(0.5 * logvar)
eps = torch.randn_like(std)
return mu + eps * std
def decode(self, z):
# デコーダのフォワードパス
h = F.relu(self.decoder_h(z))
return torch.sigmoid(self.decoder_mean(h))
def forward(self, x):
# エンコード → サンプリング → デコード
mu, logvar = self.encode(x)
z = self.reparameterize(mu, logvar)
return self.decode(z), mu, logvar
# 損失関数の定義
def loss_function(recon_x, x, mu, logvar):
# 再構築誤差とKLダイバージェンスの計算
xent_loss = F.binary_cross_entropy(recon_x, x, reduction='sum')
kl_loss = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
return (xent_loss + kl_loss) / x.size(0)
# VAEのインスタンス化とオプティマイザの定義
vae = VAE()
optimizer = optim.RMSprop(vae.parameters(), lr=0.001)
# 訓練ロスと検証ロスの履歴
train_loss_history = []
test_loss_history = []
# エポックごとの訓練と評価
for epoch in range(epochs):
# 訓練モード
vae.train()
train_loss = 0
for batch_idx, (data, _) in enumerate(train_loader):
# 勾配の初期化
optimizer.zero_grad()
# フォワードパス
recon_batch, mu, logvar = vae(data)
# 損失の計算
loss = loss_function(recon_batch, data, mu, logvar)
# バックプロパゲーション
loss.backward()
# オプティマイザの更新
train_loss += loss.item()
optimizer.step()
train_loss /= len(train_loader.dataset)
train_loss_history.append(train_loss)
# 評価モード
vae.eval()
test_loss = 0
with torch.no_grad():
for data, _ in test_loader:
recon_batch, mu, logvar = vae(data)
test_loss += loss_function(recon_batch, data, mu, logvar).item()
test_loss /= len(test_loader.dataset)
test_loss_history.append(test_loss)
print(f'Epoch: {epoch}, Train Loss: {train_loss:.4f}, Test Loss: {test_loss:.4f}')
# 計算過程の描画
df_log = pd.DataFrame({"train_loss": train_loss_history, "val_loss": test_loss_history})
df_log.plot(style=['r--', 'r-'])
plt.ylabel("Loss")
plt.xlabel("epochs")
plt.show()
データのロード: MNISTデータセットをロードしています。train=Trueは訓練データセット、train=Falseはテストデータセットを意味します。
データの整形: 28x28の画像データを784次元のベクトルに変換し、正規化(0〜1の範囲)しています。
ハイパーパラメータの定義: 学習に必要なハイパーパラメータを設定しています。
DataLoaderの作成: 訓練データとテストデータをバッチごとに取得するためのDataLoaderを作成しています。
VAEの定義: VAE(変分オートエンコーダ)のクラスを定義しています。エンコーダ部分、デコーダ部分、潜在変数のサンプリングが含まれています。
損失関数の定義: 再構築誤差とKLダイバージェンスを計算する損失関数を定義しています。
モデルのインスタンス化とオプティマイザの設定: VAEのインスタンスを作成し、RMSpropオプティマイザを設定しています。
訓練ループ: エポックごとに訓練データを通してVAEを訓練し、テストデータで評価しています。訓練と検証の損失の履歴も保存しています。
結果の描画: 訓練と検証の損失をエポックごとにプロットして表示しています。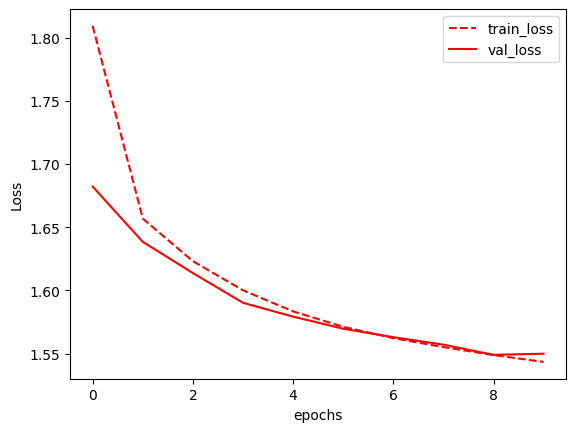
# 評価モードに設定 (DropoutやBatchNormを無効化)
vae.eval()
# テストデータを潜在空間にエンコード
# torch.no_grad()は勾配計算を無効化してメモリ使用量を減らす
with torch.no_grad():
x_test_encoded = torch.cat([vae.encode(data)[0] for data, _ in test_loader])
# 2次元プロット作成
# x_test_encodedの各行は潜在空間の2次元ベクトル
# y_testのargmaxを使用して正解ラベルを取得
plt.figure(figsize=(6, 6))
plt.scatter(x_test_encoded[:, 0], x_test_encoded[:, 1], c=torch.argmax(y_test, axis=1))
plt.xlabel("z_mean[0]") # 潜在変数の平均の1次元目
plt.ylabel("z_mean[1]") # 潜在変数の平均の2次元目
plt.colorbar() # カラーバーの追加
plt.show()
評価モードの設定: vae.eval()でVAEモデルを評価モードに設定します。これにより、訓練時のみに使われる層(例:Dropout、Batch Normalization)が無効化されます。
勾配計算の無効化: with torch.no_grad():は、このブロック内での勾配計算を無効化します。これにより、メモリ使用量を減らし、計算速度を向上させることができます。
テストデータのエンコード: vae.encode(data)[0]でテストデータを潜在空間にエンコードし、潜在変数の平均(z_mean)を取得します。これらの平均ベクトルを結合して、全テストデータの潜在表現を作成します。
2次元プロットの作成: plt.scatterを使用して、潜在変数の平均を2次元空間にプロットします。各点の色は、対応するデータポイントの正解ラベル(0から9)に基づいており、torch.argmax(y_test, axis=1)で取得しています。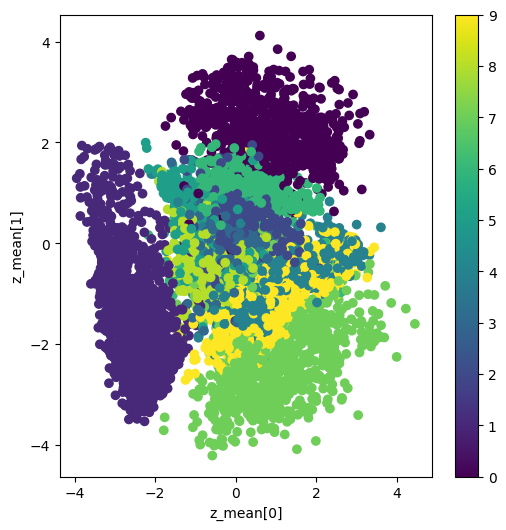
# グリッドのサイズと画像のサイズを設定
n = 15
digit_size = 28
# figure配列を初期化。これは生成された画像を格納するための配列です
figure = np.zeros((digit_size * n, digit_size * n))
# 潜在空間のグリッドを作成。-5から5の範囲でn個の点を生成
grid_x = np.linspace(-5, 5, n)
grid_y = np.linspace(-5, 5, n)
# 勾配計算を無効化するコンテキスト内で実行
with torch.no_grad():
# grid_xとgrid_yの各座標を反復処理
for i, xi in enumerate(grid_x):
for j, yi in enumerate(grid_y):
# 潜在変数として使用する2次元ベクトルを作成
z_sample = torch.tensor([[xi, yi]], dtype=torch.float)
# デコーダを使用して潜在変数から画像を生成
x_decoded = vae.decode(z_sample)
# 生成された画像を28x28に整形
digit = x_decoded[0].reshape(digit_size, digit_size)
# figure配列に生成された画像を追加
figure[(n-1-j) * digit_size: (n-1-j+1) * digit_size, i * digit_size: (i+1) * digit_size] = digit
# 最終的な画像を表示。これにより潜在空間がどのように画像にマッピングされるかがわかります
plt.figure(figsize=(10, 10))
plt.imshow(figure, cmap='Greys_r')
plt.yticks(np.arange(0, n*28, 28), grid_y[::-1].round(1)) # y軸のラベル
plt.xticks(np.arange(0, n*28, 28), grid_x.round(1)) # x軸のラベル
plt.xlabel("x") # x軸の名前
plt.ylabel("y") # y軸の名前
plt.show() # グラフの表示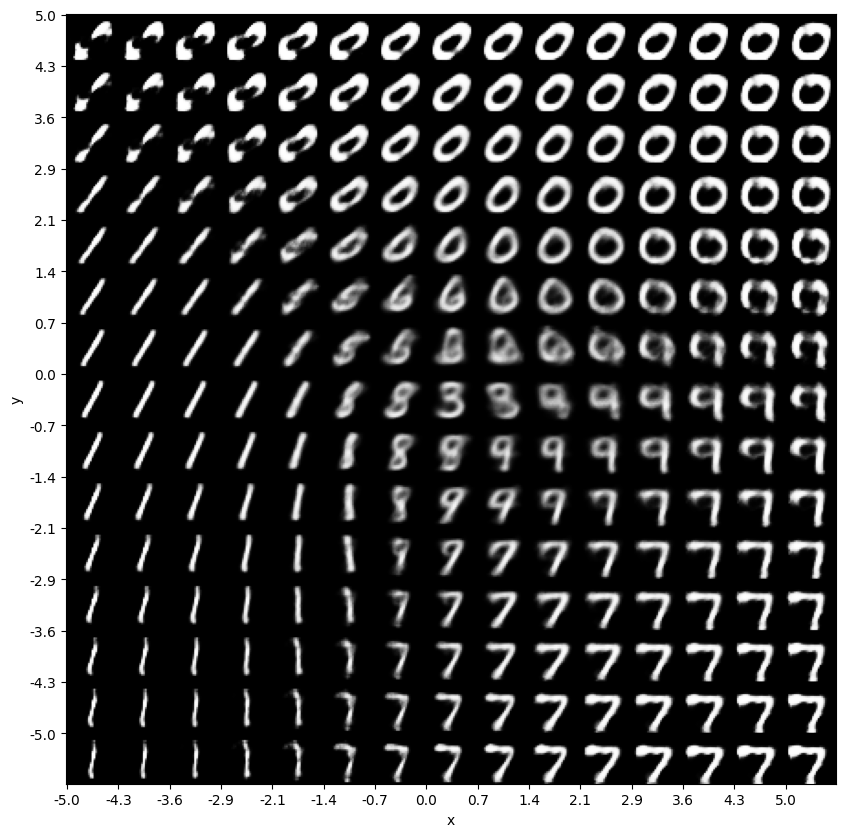
まとめ
最後までご覧いただきありがとうございました。
