【G検定】相関係数

【G検定まとめ】要点整理＆当日用カンペの項目別詳解ページです。

詳細な知識や実装は試験には必ずしも必須ではありませんが、試験対策として理解を深めたい方はぜひ最後までご覧ください。

G検定まとめはこちら

相関係数

互いの特徴量の相関の正負と強さを表す指標のこと。1に近いほど強い正の相関、−1に近いほど負の相関を持つ。

相関係数

相関係数は、2 つの変数間の線形関係の強さと方向を表す統計的尺度です。通常は記号 “r” で表され、-1 から +1 の間の値をとります。+1 の相関係数は、完全な正の線形関係を示します。つまり、1 つの変数が増加すると、他の変数も増加します。-1 の相関係数は、完全な負の線形関係を示します。つまり、一方の変数が増加すると、もう一方の変数が減少します。相関係数 0 は、2 つの変数間に線形関係がないことを示します。

相関係数はデータ分析で一般的に使用され、変数間の関係の識別、傾向の検出、および予測を行うための重要なツールです。金融、経済、心理学、社会学などの分野で広く使用されています。

相関係数の例

たとえば、学生の勉強量と試験の点数との相関関係を判断したいとします。10 人の学生のデータを収集し、毎週の勉強時間と試験の点数を記録することができました。次に、2 つの変数間の相関係数を計算できます。

相関係数が 1 の場合、完全な正の相関があることを示します。つまり、勉強した時間が増えると、試験の点数も上がります。相関係数が -1 の場合、完全な負の相関があることを示します。つまり、学習時間が増えると、試験の点数が低下します。相関係数が 0 の場合は、相関がないことを示し、勉強量と試験の点数には関係がないことを意味します。

相関係数の計算方法の例を次に示します。

学生	学習時間	試験の点数
1	5	80
2	4	75
3	7	90
4	2	60
5	3	70
6	8	95
7	6	85
8	1	50
9	9	100
10	2	65

相関係数を計算するには、まず 2 つの変数の平均を計算します。

$$学習時間の平均 = (5+4+7+2+3+8+6+1+9+2)/10 = 4.7 $$ $$試験スコアの平均 = (80+75+90+60+70+95+85+ 50+100+65)/10 = 77$$

次に、2 つの変数の標準偏差を計算します。

$$学学習時間の標準偏差 = 2.46$$ $$ 試験の点数の標準偏差 = 17.99$$

最後に、次の式を使用して相関係数を計算します。

$$相関係数 = Σ((x – x̄) * (y – Å)) / (n-1) * Sx * Sy$$ $$x と y は 2 つの変数の値、x̄ と ȳ はそれらの平均値、n はサンプルサイズ、Sx と Sy はそれらの標準偏差です。$$

この例の値を差し込むと、次のようになります。

$$相関係数 = ((5-4.7) (80-77) + (4-4.7) (75-77) + (7-4.7) (90-77) + (2-4.7) (60-77) + (3 -4.7) (70-77) + (8-4.7) (95-77) + (6-4.7) (85-77) + (1-4.7) (50-77) + (9-4.7) (100- 77) + (2-4.7) (65-77)) / 9 * 2.46 * 17.99$$ $$相関係数 = 0.889$$

相関係数が1に近いことから、勉強量と試験の点数との間に強い正の相関があることを示しています。

相関関係と因果関係

相関係数は、2 つの変数間の線形関係の強さと方向を表す統計的尺度です。範囲は -1 から 1 で、相関係数 -1 は完全な負の関係を示し、0 は関係がないことを示し、1 は完全な正の関係を示します。

一方、因果関係とは、ある出来事 (原因) と 2 つ目の出来事 (結果) の関係を指し、2 つ目の出来事は最初の出来事の結果です。言い換えれば、因果関係は、ある変数の変化が別の変数の変化を引き起こす原因であることを示唆しています。

相関関係と因果関係は関連していますが、相関関係は必ずしも因果関係を意味するわけではありません。2 つの変数間の強い相関関係は、因果関係の存在を示唆する場合がありますが、因果関係を証明するものではありません。両方の変数に影響を与える他の要因または変数が存在する可能性があります。これは、相関関係が偶然または誤っている可能性があることを意味します。

因果関係を確立するには、時間的な優先順位 (原因が結果よりも前に来る必要がある)、妥当性 (原因と結果が論理的に理にかなっている必要がある)、および一貫性 (原因と結果が既存の知識に適合する必要がある) などの追加の基準を満たす必要があります。さらに、変数が操作および制御される実験計画は、観察研究よりも因果関係をより明確に確立するのに役立ちます。

相関は 2 つの変数間の関係の強さと方向の尺度であり、因果関係は変数間の因果関係の存在を指します。相関関係は必ずしも因果関係を意味するわけではなく、因果関係を確立するには、強い相関関係を超えた追加の基準を満たす必要があります。

相関係数の欠点

相関係数は、2 つの変数間の線形関係の強さと方向を表す、広く使用されている統計的尺度です。これは多くの設定で便利なツールですが、次のような制限や潜在的な欠点があることに注意してください。

相関関係は因果関係を意味するものではありません: 相関係数は 2 つの変数間の線形関係の強さを測定するだけで、因果関係を確立するものではありません。つまり、2 つの変数が強く相関しているからといって、一方が他方を引き起こすとは限りません。
非線形関係は捕捉されません: 相関係数は、2 つの変数間の線形関係のみを測定します。関係が非線形である場合、相関係数は誤解を招くか、完全に不正確である可能性があります。たとえば、2 つの変数間の関係が U 字型または逆 U 字型の場合、相関係数は、実際には関係が存在する場合でも関係がないことを示唆している可能性があります。
外れ値は結果を歪める可能性があります: 相関係数は外れ値に敏感です。外れ値は、残りのデータから遠く離れた極端なデータポイントです。データに外れ値がある場合、相関係数はこれらのポイントによって大きく影響を受ける可能性があり、誤解を招く結果につながります。
相関関係は、他のタイプの関係の強さを測定しません。相関係数は、2 つの変数間の線形関係の強さのみを測定します。2 つの変数間に曲線関係、単調関係、またはより複雑な関係がある場合、相関係数はこれらの関係の強さを捉えません。
相関係数は、変数の範囲と分布の影響を受ける可能性があります: 相関係数は、調査対象の変数の範囲と分布の影響を受けます。変数の 1 つが範囲が限られているか、大きく歪んでいる場合、相関係数が人為的に低くまたは高くなり、誤解を招く可能性があります。
相関は交絡変数を考慮しません: 相関係数は 2 つの変数間の関係のみを測定し、両方に関連する可能性のある他の変数の効果を考慮しません。変数を交絡させると、2 つの変数間の関係が実際よりも強くなったり弱くなったりすることがあります。

相関係数は 2 つの変数間の線形関係を説明するための有用な尺度ですが、結果を解釈する際には、その限界と潜在的な欠点を考慮することが重要です。

相関係数の算出

ここからは相関係数の算出例を紹介します。「seaborn」ライブラリと自動車の燃料効率のデータセットを使用して、Python で相関係数を見つける方法の例を次に示します。

import seaborn as sns
import matplotlib.pyplot as plt

# load the fuel efficiency dataset from seaborn
mpg = sns.load_dataset("mpg")

# calculate the correlation matrix
corr = mpg.corr()

# plot the correlation matrix as a heatmap
sns.heatmap(corr, annot=True, cmap='coolwarm', vmin=-1, vmax=1)
plt.title('Correlation matrix of car fuel efficiency')
plt.show()

この例では、「seaborn」ライブラリを使用して、さまざまな車の燃費に関する情報を含む「mpg」データセットを読み込みます。次に、デフォルトでピアソン相関係数を計算する「corr()」関数を使用して相関行列を計算します。最後に、seaborn の「heatmap()」関数を使用して、相関行列をヒートマップとしてプロットします。

結果の図は、セルがデータセット内の変数のペア間の相関係数を表すマトリックスを示します。各セルの色は相関の強さと方向を示し、暖色は正の相関を示し、寒色は負の相関を示します。

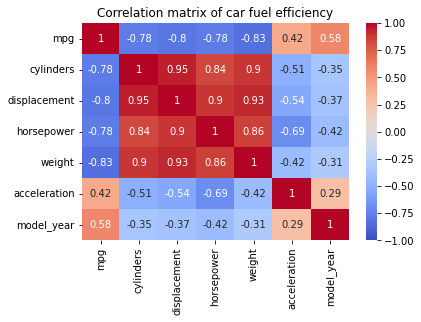
燃料効率 (mpg) とエンジン排気量 (排気量) の間には強い負の相関関係があり、燃料効率と馬力 (hp) の間には弱い負の相関関係があることがわかります。また、燃費と年式の間には中程度の正の相関があります。

G検定学習法

最後までご覧いただきありがとうございました。

当サイトではG検定に役立つ情報をまとめています。

ぜひご覧ください。

参考書籍

①教科書として使用する書籍

体系的に知識を整理することができます。

まずは、この１冊を読んでG検定の学習を進めましょう。

検索機能が使用できるので、Kindle版が特におすすめです。

②問題集として使用する書籍

ある程度学習が進んだら、本番を意識して問題集に取り組みましょう。

本番の試験環境を意識して、このページ「要点整理＆当日用カンペ」を使用しながら解答してみましょう。

カテゴリー: G検定、資格

タグ: G検定

相関係数

相関係数

相関係数の例

相関関係と因果関係

相関係数の欠点

相関係数の算出

G検定学習法

本サイトの活用方法

【G検定2024最新】試験当日も使える! 187項目の要点整理＆試験対策カンペ【新シラバス対応】

G検定シラバス改訂の概要と変更のポイント

【G検定2024まとめ】理解度確認問題集【直前対策】

【G検定まとめ2024】YouTube動画リスト（問題編）

【G検定まとめ2024】YouTube動画リスト（講義編）

【G検定まとめ2024】試験当日も使える! 要点整理＆試験対策カンペ【旧シラバス】

参考書籍

【G検定】サポートベクターマシン(SVM)

【G検定】自己回帰モデル(ARモデル)