【G検定】ウォード(Ward)法

【G検定まとめ】要点整理＆当日用カンペの項目別詳解ページです。

詳細な知識や実装は試験には必ずしも必須ではありませんが、試験対策として理解を深めたい方はぜひ最後までご覧ください。

G検定まとめはこちら

ウォード法

k-means法からさらに、クラスタの階層構造を求めるまで行う手法。最も距離が近い2つのデータ（クラスタ）を選び、それらを1つのクラスタにまとめる処理を繰り返していく。クラスタリングのまとまりを表した樹形図のことをデンドログラム（dendrogram）という。

ウォード法

Ward法は、データ分析とパターン認識で使用される階層的クラスタリングアルゴリズムです。これは、各データポイントが独自のクラスターを形成することから開始し、停止基準が満たされるまで、最も類似したクラスターを再帰的にマージするボトムアップ凝集法です。

Ward 法は、各クラスター内のすべてのポイント間の二乗距離の合計を最小化することに基づいています。各ステップで、距離の二乗和の増加が最小になる 2 つのクラスターをマージします。目的は、2 つのクラスターを組み合わせた結果生じる分散の増加を最小限に抑えることです。

Ward法は、互いに類似しているオブジェクトまたはサンプルのグループを識別することが目標である状況でよく使用されます。内部構造に関してコンパクトで比較的均一なクラスターを識別できるため、データに多くの変数または特徴が含まれている場合に特に役立ちます。

Ward法の利点の 1 つは、クラスタリングプロセスを視覚的に表現したデンドログラムを作成できることです。デンドログラムはクラスターがマージされた順序を示し、各枝の高さはマージの結果として生じる分散の増加に対応します。

ウォード法は、各クラスター内のデータポイント間の二乗距離の合計を最小化することに基づく一般的なクラスタリングアルゴリズムです。これは、類似したオブジェクトまたはサンプルのグループを識別することが目標である状況でよく使用されます。この方法は、クラスタリングプロセスを視覚的に表現するデンドログラムを生成することができます。

ウォード法

Ward 法の手順は次のとおりです。

・各観測を独自のクラスターとして扱うことから始めます。観測値の各ペア間の距離を計算します。
・クラスターの各ペアについて、それらの観測値間の二乗距離の合計を計算します。これは、クラスター内平方和 (WCSS) です。
・マージによる WCSS の増加が最も小さい 2 つのクラスターをマージします。

ウォード法とk-means法の違い

k-means 法と Ward 法はどちらも、クラスター分析で一般的に使用されます。クラスター分析は、類似のオブジェクトまたはデータポイントをグループ化するために使用される手法です。

k-means 法は、与えられた一連の観測を k 個のクラスターに分割しようとする反復アルゴリズムです。ここで、k は事前に指定された数値です。アルゴリズムは、観測値を k 個のクラスターの 1 つにランダムに割り当てることから開始し、クラスターの重心を繰り返し更新して、クラスターへの観測値の割り当てが変更されなくなるまで、最も近い重心を持つクラスターに観測値を再割り当てします。k-means 法の目的は、各観測値と割り当てられたクラスター重心との間の距離の平方和を最小化することです。

一方、Ward の方法は、クラスタリングプロセスの各ステップで、クラスタ内分散の合計 (平均からの偏差の二乗和) を最小化しようとする階層的クラスタリング方法です。この方法では、まず各観測値を個別のクラスターと見なし、クラスターが 1 つだけになるまで再帰的にクラスターをマージします。この方法では、マージの結果として生じるクラスター内分散の合計の増加を評価することにより、各ステップでどの 2 つのクラスターをマージするかを決定します。

k-means と Ward の方法の主な違いの 1 つは、k-means では事前に指定された数のクラスター (k) が必要であるのに対し、Ward の方法では必要がないことです。Ward の方法は、各観測を個別のクラスターとして開始し、クラスターが 1 つだけになるまで、最も近い 2 つのクラスターを連続的にマージします。もう 1 つの違いは、k-means は分割法であり、各観測が正確に 1 つのクラスターに割り当てられることを意味しますが、Ward の方法は階層法であり、各観測が階層の異なるレベルで複数のクラスターに属することができることを意味します。

k-means と Ward の方法はどちらもクラスター分析で広く使用されていますが、クラスター化へのアプローチとデータに関する仮定が異なります。K-means は、観測値と割り当てられたクラスター重心との間の距離の平方和を最小化しようとする分割方法であり、Ward の方法は、クラスタリングプロセスの各ステップでクラスター内分散の合計を最小化しようとする階層的方法です。

ウォード法の活用例

顧客のセグメンテーション: Ward の方法を使用して、購入行動に基づいて顧客をセグメント化できます。同様の購入パターンを共有する顧客をクラスター化することにより、企業はマーケティングおよび販売戦略を調整して、各グループをより効果的にターゲットにすることができます。
画像のセグメンテーション: 画像処理では、ウォードの方法を使用して、画像の色、テクスチャ、またはその他の特徴に基づいて画像をセグメント化できます。たとえば、類似性に基づいてピクセルをグループ化し、画像内の異なる領域を識別するために使用できます。
遺伝子発現解析: バイオインフォマティクスでクラスター化に使用されます

ウォード法の実装

import numpy as np
import pandas as pd
from scipy.spatial.distance import pdist, squareform
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt

クラスター化するデータセットをロードする必要があります。この例では、3 種類のアヤメの花の花弁と萼片の寸法に関する情報を含む Iris データセットを使用します。

iris = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', header=None)
X = iris.iloc[:, :-1].values

ユークリッド距離メトリックを使用して、すべてのサンプル間のペアごとの距離を計算します。

dist = pdist(X, metric='euclidean')

次に、次の関数を使用してペアごとの距離を平方距離行列に変換します。

dist_matrix = squareform(dist)

この距離行列にウォード法を適用します。

linkage_matrix = linkage(dist_matrix, method='ward')

最後に、関数を使用して結果のデンドログラムを視覚化できます。

plt.figure(figsize=(20, 14))
dendrogram(linkage_matrix)
plt.show()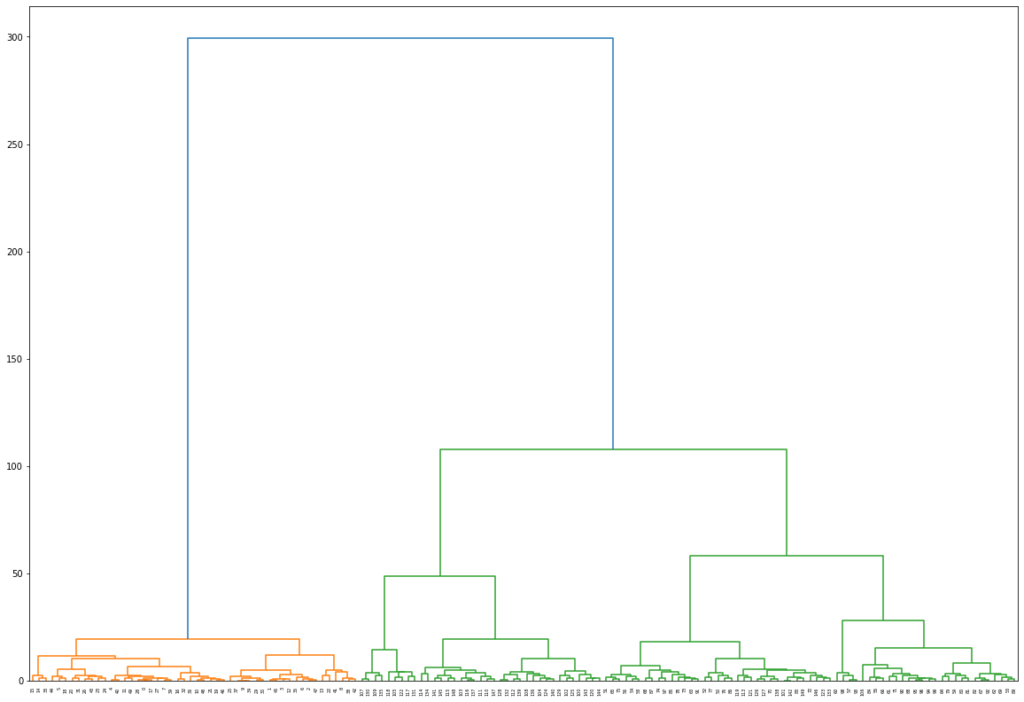

G検定学習法

最後までご覧いただきありがとうございました。

当サイトではG検定に役立つ情報をまとめています。

ぜひご覧ください。

参考書籍

①教科書として使用する書籍

体系的に知識を整理することができます。

まずは、この１冊を読んでG検定の学習を進めましょう。

検索機能が使用できるので、Kindle版が特におすすめです。

②問題集として使用する書籍

ある程度学習が進んだら、本番を意識して問題集に取り組みましょう。

本番の試験環境を意識して、このページ「要点整理＆当日用カンペ」を使用しながら解答してみましょう。

ウォード法

ウォード法

ウォード法

ウォード法とk-means法の違い

ウォード法の活用例

ウォード法の実装

G検定学習法

本サイトの活用方法

【G検定まとめ2024】試験当日も使える! 要点整理＆試験対策カンペ【動画】

【G検定まとめ2024】試験当日も使える! 要点整理＆試験対策カンペ

【G検定2023まとめ】理解度確認&問題集まとめ【直前対策】

【G検定2023】G検定の概要と試験のポイント

【G検定】G検定合格体験記　〜学習方法と受験体験〜

【G検定2022】シラバスでみるG検定の試験内容

参考書籍

関連

【E資格】シラバスでみるE資格の試験内容（E2022#2〜）

【G検定】ディープブルー