このシリーズではE資格対策として、書籍「ゼロから作るDeep Learning」を参考に学習に役立つ情報をまとめています。
<参考書籍>
計算グラフとは
計算グラフは、複雑な計算やアルゴリズムを視覚的に表現し、理解しやすくする手法です。機械学習やディープラーニングの分野でよく使われ、ノードとエッジという二つの要素で構成されています。
ノードは、計算グラフの基本単位で、関数や変数、定数などを示します。ノードは数値を受け取り、それを元に何らかの計算を行い、結果を出力します。一方、エッジはノード間の線であり、データがどのように流れるかを示します。エッジは矢印で表され、データの流れの方向性を明確にします。
計算グラフを使用することで、複雑な計算の過程を直感的に理解することができます。さらに、計算グラフは逆伝播アルゴリズムや自動微分といった重要な概念の導入にも役立ちます。これにより、ニューラルネットワークの学習において勾配を効率的に計算することが可能になります。
- ノード (Node): ノードは、計算グラフの基本要素であり、通常、関数や変数、定数などを表現します。具体的には、ノードには数値が入力され、何らかの計算を行った結果が出力されます。例えば、ノードが加算関数である場合、2つの数値が入力され、その和が出力されます。
- エッジ (Edge): エッジは、ノード間の関係を表現する線で、計算グラフにおいてデータが流れる道を示します。エッジは、一つのノードから別のノードへのデータの移動を示すために使用されます。通常、エッジは矢印で描かれ、データの流れの方向を示します。
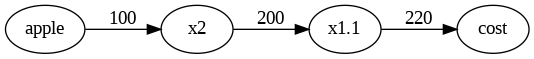
計算グラフを使用することで、複雑な計算やアルゴリズムを視覚化し、理解しやすくなります。また、計算グラフは逆伝播(バックプロパゲーション)アルゴリズムや自動微分などの概念を導入する際にも非常に役立ちます。
計算グラフの作図
例1
簡単な問題を計算グラフを使って解いていきます。
問1:Aさんは1個100円のリンゴを2個買いました。その際の支払い金額を求めなさい。ただし、消費税は10%とする。
この問題に対する計算グラフは以下のように実装することで出力することができます。
!apt-get install graphviz
!pip install graphvizfrom graphviz import Digraph
# 計算グラフの構造を定義
g = Digraph('G', filename='simple_calculate_graph_horizontal.gv', format='png', graph_attr={'rankdir': 'LR'})
# ノードの追加
g.node('apple')
g.node('×2')
g.node('×1.1')
g.node('cost')
# エッジの追加
g.edge('apple', '×2', label='100')
g.edge('×2', '×1.1', label='200')
g.edge('×1.1', 'cost', label='220')
# 計算グラフを横向きに画像として出力
g.render()実行結果:
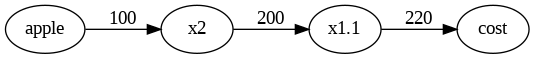
例2
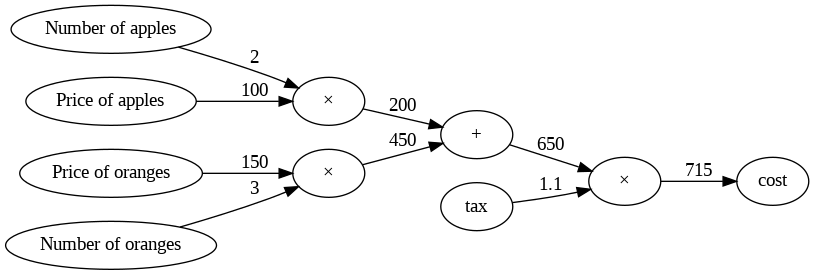
問2:Aさんは1個100円のリンゴを2個、1個150円のみかんを3個買いました。その際の支払い金額を求めなさい。ただし、消費税は10%とする。
from graphviz import Digraph
# 計算グラフの構造を定義
g = Digraph('G', filename='simple_calculate_graph_horizontal.gv', format='png', graph_attr={'rankdir': 'LR'})
# ノードの追加
g.node('A','Number of apples')
g.node('B','Price of apples')
g.node('C','×')
g.node('D','Number of oranges')
g.node('E','Price of oranges')
g.node('F','×')
g.node('G','+')
g.node('H','tax')
g.node('I','×')
g.node('J','cost')
# エッジの追加
g.edge('A', 'C', label='2')
g.edge('B', 'C', label='100')
g.edge('D', 'F', label='3')
g.edge('E', 'F', label='150')
g.edge('C', 'G', label='200')
g.edge('F', 'G', label='450')
g.edge('G', 'I', label='650')
g.edge('H', 'I', label='1.1')
g.edge('I', 'J', label='715')
# 計算グラフを横向きに画像として出力
g.render()実行結果:
なぜ計算グラフを使うのか
計算グラフは、複雑な計算をより簡単な局所的な計算に分解する能力を持っています。これは、大規模な計算の効率的な実行を可能にし、計算の処理速度を向上させます。さらに、計算グラフは個々の計算の依存関係を明確に示すことができるため、並列計算の実行や最適化の過程を容易に進めることができます。
計算グラフ上で、順伝播は、ノードに対応する関数を適用し、エッジを通じてデータを伝搬させることで表現されます。一方で、逆伝播は損失ノードから入力ノードまでの逆向きの伝搬として表現され、連鎖律(チェーンルール)を利用して各ノードにおける勾配を効率的に計算します。
まとめ
最後までご覧いただきありがとうございました。

