このシリーズではE資格対策として、書籍「ゼロから作るDeep Learning」を参考に学習に役立つ情報をまとめています。

<参考書籍>

目次

連鎖律とは

ニューラルネットワークでは、複雑な合成関数が各層で形成されます。計算グラフを用いることで、この合成関数の構成要素や順序を視覚的に理解しやすくなります。そして、連鎖律を適用することで、計算グラフ上に表現された各関数の微分を効率的に求めることができます。

特に、ニューラルネットワークの学習では、出力と正解の誤差を用いて、重みやバイアスといったパラメータを更新していく必要があります。この際、連鎖律を使って誤差の勾配を計算し、計算グラフ上で逆方向に伝播させることで、各パラメータの更新量を求めます。

合成関数の微分について考える

$$z = (x + y)^2$$

この式は以下のように構成されている。

$$z = t^2,$$ $$t = x + y $$

連鎖律（chain rule）は、合成関数の微分に関する重要なルールです。合成関数とは、複数の関数を組み合わせてできる関数のことを指します。例えば、関数 f(x) と g(x) がある場合、合成関数は

$$ h(x) = f(g(x))$$

のように表現されます。

連鎖律の概要は次のようになります

$$ (h ◦ g)'(x) = h'(g(x)) * g'(x)$$

ここで、h'(x) は関数 h(x) の導関数（微分）を表し、g'(x) は関数 g(x) の導関数（微分）を表します。

連鎖律を適用するために、まずそれぞれの関数の導関数を求めます。z = t^2 について、t で微分すると、

$$\frac{∂z}{∂t}= 2t$$

次に、t = x + y について、x で微分すると、

$$\frac{∂t}{∂x}= 1$$

また、y で微分すると、

$$\frac{∂t}{∂y}= 1$$

これで必要な導関数がすべて揃いました。連鎖律を適用して、z を x で微分すると、

$$\frac{∂z}{∂x} = \frac{∂z}{∂t} * \frac{∂t}{∂x}= 2t * 1 = 2(x + y)$$

同様に、z を y で微分すると、

$$\frac{∂z}{∂y}= \frac{∂z}{∂t} *\frac{∂t}{∂y}= 2t * 1 = 2(x + y)$$

以上のように、連鎖律を使って合成関数 z を x および y で微分することができました。このように連鎖律は、合成関数の微分を行う際に非常に便利な法則です。

連鎖律と計算グラフ

先ほどの式の連鎖律の計算を計算グラフで表してみます。

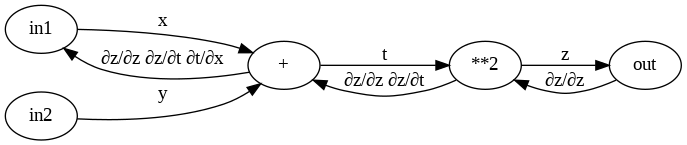
逆伝播の計算手順では右から左に信号を伝播していきます。

これを先ほど微分の結果を当てはめる、以下のようになります。

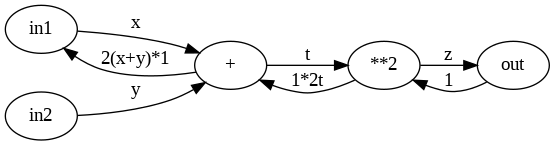
逆伝播と計算グラフ

加算ノードの逆伝播

順伝播
逆伝播

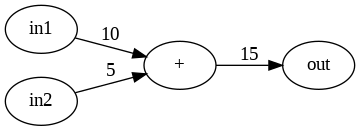
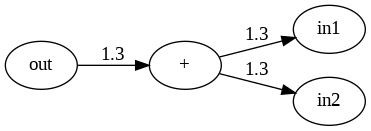
乗算ノードの逆伝播

順伝播
逆伝播

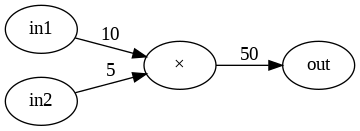
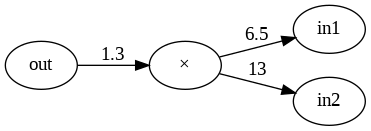
乗算レイヤの実装

乗算レイヤの実装例を以下に示します。このコードでは、MulLayerクラスを定義し、順伝播（forwardメソッド）と逆伝播（backwardメソッド）の処理を実装しています。initメソッドでは、乗算レイヤーの入力値xおよびyを初期化しています。forwardメソッドでは、xとyの乗算結果を計算し、backwardメソッドでは、逆伝播に必要な偏微分値dxおよびdyを計算しています。

# MulLayer クラスを定義
class MulLayer:
    # コンストラクタ
    def __init__(self):
        # 入力値 x と y を初期化（None で初期化）
        self.x = None
        self.y = None

    # forward メソッド（順伝播）を定義
    def forward(self, x, y):
        # 入力値 x と y をインスタンス変数に格納
        self.x = x
        self.y = y
        # 乗算結果を計算し、 out に格納
        out = x * y
        # 乗算結果を返す
        return out

    # backward メソッド（逆伝播）を定義
    def backward(self, dout):
        # dx を計算（dout に self.y を掛ける）
        dx = dout * self.y
        # dy を計算（dout に self.x を掛ける）
        dy = dout * self.x
        # dx と dy を返す
        return dx, dy

以下の例を使用して乗算レイヤを実装してみます。このコードは、りんごの価格と消費税を考慮して最終価格を計算し、各変数に対する微分を求めるサンプルです。MulLayerクラスは乗算を行うレイヤで、順伝播(forward)と逆伝播(backward)の機能を持っています。

Aさんは１個100円のリンゴを2個買いました。その際の支払い金額を求めなさい。ただし、消費税は10％とする。

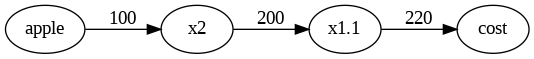
# 変数を定義
apple = 100  # リンゴの単価
apple_num = 2  # リンゴの個数
tax = 1.1  # 消費税率（10%）

# MulLayer クラスのインスタンスを生成
mul_apple_layer = MulLayer()  # リンゴの価格を計算するレイヤー
mul_tax_layer = MulLayer()  # 税込価格を計算するレイヤー

# 順伝播（forward）
# リンゴの価格を計算（リンゴの単価 × リンゴの個数）
apple_price = mul_apple_layer.forward(apple, apple_num)
# 税込み価格を計算（リンゴの価格 × 消費税率）
price = mul_tax_layer.forward(apple_price, tax)

# 逆伝播（backward）
dprice = 1  # 価格の微分
# 税込み価格に対するリンゴ価格と消費税率の微分を計算
dapple_price, dtax = mul_tax_layer.backward(dprice)
# リンゴ価格に対するリンゴ単価とリンゴ個数の微分を計算
dapple, dapple_num = mul_apple_layer.backward(dapple_price)

# 結果を出力
print("price:", int(price))  # 税込み価格
print("dApple:", dapple)  # リンゴ単価の微分
print("dApple_num:", int(dapple_num))  # リンゴ個数の微分
print("dTax:", dtax)  # 消費税率の微分

実行結果:

price: 220
dApple: 2.2
dApple_num: 110
dTax: 200

加算レイヤの実装

加算レイヤの実装例を以下に示します。このAddLayerクラスは、順伝播（forward）で2つの入力値（x, y）を加算し、逆伝播（backward）でそれぞれの入力値に対する微分（勾配）を計算します。加算において、微分は1になるため、backwardメソッドでは、引数として渡された微分（dout）に1をかけています。

class AddLayer:
    # コンストラクタ
    def __init__(self):
        pass  # 初期化は特に行わない

    # 順伝播（forward）
    def forward(self, x, y):
        out = x + y  # 入力された x と y を加算

        return out   # 加算結果を返す

    # 逆伝播（backward）
    def backward(self, dout):
        dx = dout * 1  # x に関する微分を計算 (加算に関しては微分が 1)
        dy = dout * 1  # y に関する微分を計算 (加算に関しては微分が 1)

        return dx, dy  # x, y の微分結果を返す

以下の例を使用して乗算レイヤを実装してみます。リンゴとオレンジの価格を考慮して消費税込みの合計金額を計算し、それぞれの変数に対する微分（勾配）を求めることを目的としています。

Aさんは１個100円のリンゴを2個、1個150円のみかんを3個買いました。その際の支払い金額を求めなさい。ただし、消費税は10％とする。

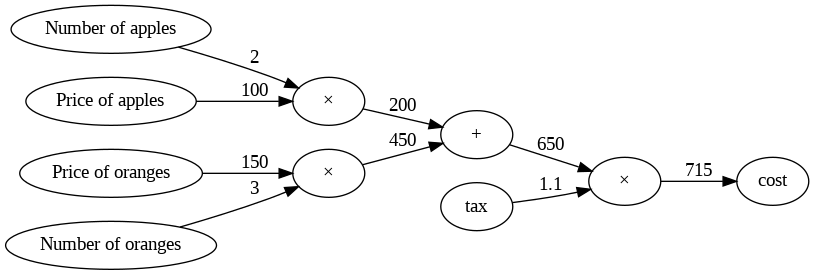
# 変数を定義
apple = 100  # リンゴの単価
apple_num = 2  # リンゴの個数
orange = 150  # オレンジの単価
orange_num = 3  # オレンジの個数
tax = 1.1  # 消費税率（10%）

# 各レイヤーを作成
mul_apple_layer = MulLayer()  # リンゴの価格を計算するレイヤー
mul_orange_layer = MulLayer()  # オレンジの価格を計算するレイヤー
add_apple_orange_layer = AddLayer()  # リンゴとオレンジの価格を合算するレイヤー
mul_tax_layer = MulLayer()  # 税込価格を計算するレイヤー

# 順伝播（forward）
apple_price = mul_apple_layer.forward(apple, apple_num)  # (1) リンゴの価格を計算
orange_price = mul_orange_layer.forward(orange, orange_num)  # (2) オレンジの価格を計算
all_price = add_apple_orange_layer.forward(apple_price, orange_price)  # (3) リンゴとオレンジの価格を合算
price = mul_tax_layer.forward(all_price, tax)  # (4) 税込み価格を計算

# 逆伝播（backward）
dprice = 1  # 価格の微分
dall_price, dtax = mul_tax_layer.backward(dprice)  # (4) 税込み価格に対する各変数の微分を計算
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price)  # (3) 合計価格に対する各変数の微分を計算
dorange, dorange_num = mul_orange_layer.backward(dorange_price)  # (2) オレンジ価格に対する各変数の微分を計算
dapple, dapple_num = mul_apple_layer.backward(dapple_price)  # (1) リンゴ価格に対する各変数の微分を計算

# 結果を出力
print("price:", int(price))  # 税込み価格
print("dApple:", dapple)  # リンゴ単価の微分
print("dApple_num:", int(dapple_num))  # リンゴ個数の微分
print("dOrange:", dorange)  # オレンジ単価の微分
print("dOrange_num:", int(dorange_num))  # オレンジ個数の微分
print("dTax:", dtax)  # 消費税率の微分

実行結果:

price: 715
dApple: 2.2
dApple_num: 110
dOrange: 3.3
dOrange_num: 165
dTax: 650

まとめ

最後までご覧いただきありがとうございました。

カテゴリー
E資格、資格
タグ
前の記事
【E資格】第11回:計算グラフの考え方【ゼロから作るDeep Learning】
2023年4月2日
次の記事
【E資格】第13回:ReLUレイヤとSigmoidレイヤ【ゼロから作るDeep Learning】
2023年4月4日