このシリーズではE資格対策として、シラバスの内容を項目別にまとめています。

E資格まとめ

試験概要 ディープラーニングの理論を理解し、適切な手法を選択して実装する能力や知識を有しているかを認定する。 １．応用数学 （１）確率・統計 （２）情報理論 ２．機…

つくもちブログ　〜Python&AIまとめ〜
目次

Momentumとは

モメンタムとは、機械学習の最適化手法における一つの概念で、特にニューラルネットワークの学習においてよく使用されます。

まず、基本的な勾配降下法について説明します。勾配降下法とは、機械学習モデルのパラメータを最適化するための手法で、損失関数（モデルの出力と真の値との差を示す関数）の勾配（傾き）を使ってパラメータを更新します。具体的には、損失関数が最小になる方向（つまり、勾配が最も急な方向の逆方向）へパラメータを少しずつ移動させていきます。

しかし、この基本的な勾配降下法にはいくつかの問題があります。例えば、損失関数が「谷」の形状をしている場合、最適な解（最小値）に到達するのに時間がかかることがあります。これは、谷の両側の勾配が互いに打ち消し合い、パラメータの更新が遅くなるためです。

ここでモメンタムの概念が登場します。モメンタムは、物理学における運動量の概念を模倣したもので、前回のパラメータの更新量（「速度」）を考慮に入れることで、パラメータの更新が一定の「勢い」を持つようにします。つまり、一度決定した方向に対して一貫性を持たせるような効果があります。

モメンタムを使用すると、前述の「谷」の問題を効果的に解決できます。谷の両側の勾配が互いに打ち消し合う現象に対して、モメンタムは前回の更新方向（「下り坂」の方向）を考慮に入れるため、パラメータの更新が一定の方向性を維持しやすくなります。結果として、最適な解に早く収束することが期待できます。

具体的な数式では、モメンタム付き勾配降下法は以下のように表されます：

1. 速度の更新：

$$ \begin{align*} v(t+1) & = \beta v(t) – \alpha \nabla L(\theta(t)) \end{align*} $$

2. パラメータの更新：

\begin{align*} \theta(t+1) & = \theta(t) + v(t+1) \end{align*}

ここで、

  • v(t)は時刻tにおける速度（パラメータの更新量）
  • βはモメンタム係数（通常は0.9などの値を使う）
  • αは学習率
  • ∇L(θ(t))は時刻tにおける損失関数の勾配
  • θ(t)は時刻tにおけるパラメータ

となります。

この式からわかるように、モメンタム付き勾配降下法では、パラメータの更新量v(t+1)が、前回の更新量v(t)と現在の勾配に基づいて計算されます。βv(t)の部分が「運動量」に相当し、これにより更新量が一定の方向性を維持することが可能になります。また、-α∇L(θ(t))の部分は、現在の勾配に基づいてパラメータを更新する部分です。

最終的に、パラメータθはこの更新量v(t+1)によって更新されます。これにより、パラメータの更新が「勢い」を持つようになり、最適な解に早く収束することが期待できます。

モメンタムの利点は、勾配が極端に小さい場合や、局所的な最小値に陥りがちな問題に対して、より良い性能を発揮する点にあります。

Momentumの実装

モメンタム最適化を行う際に使用するパラメータを更新するためのクラスを定義します。パラメータの更新は、updateメソッドを通じて行われ、モメンタム法の更新則に従って更新速度vが計算され、それに基づいてパラメータが更新されます。

class Momentum:

    """Momentum SGD"""

    # コンストラクタ：インスタンスが作成される際に初めて実行される特殊なメソッド
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr  # 学習率の設定。デフォルトは0.01
        self.momentum = momentum  # モメンタムの値の設定。デフォルトは0.9
        self.v = None  # パラメータの更新速度を保存するための辞書。初期状態ではNone
        
    # パラメータの更新を行うメソッド
    def update(self, params, grads):
        # self.vがNoneの場合（つまり初回の更新時）、self.vを初期化
        if self.v is None:
            self.v = {}  # self.vを空の辞書として初期化
            # paramsの各要素に対して、同じ形状のゼロ配列をvの初期値とする
            for key, val in params.items():                                
                self.v[key] = np.zeros_like(val)
                
        # 全てのパラメータに対して更新を行う
        for key in params.keys():
            # モメンタムの更新則に基づき、更新速度vを計算
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] 
            # 更新速度vに基づいてパラメータを更新
            params[key] += self.v[key]
  1. __init__(self, lr=0.01, momentum=0.9): これはクラスの初期化関数です。この関数は、学習率(lr)とモメンタムの値(momentum)を引数として受け取り、それらをインスタンス変数として保存します。また、self.vはモメンタム用の辞書で、パラメータの更新速度を保存するために使用されます。初期状態ではNoneとなっています。
  2. update(self, params, grads): これはパラメータを更新するための関数です。引数として現在のパラメータ(params)とその勾配(grads)を受け取ります。
  3. if self.v is None:: これはself.vが初期化されていない場合（つまり初回の更新時）に実行される処理です。各パラメータに対応する更新速度を保存するための辞書を初期化します。具体的には、各パラメータの形状と同じだけのゼロ配列を作ります。
  4. for key in params.keys():: これは全てのパラメータに対して更新を行うためのループです。
  5. self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]: これはモメンタム最適化の更新則に基づいて更新速度を計算する部分です。現在の更新速度(self.v[key])にモメンタムを掛け、そこから学習率と勾配の積を引きます。
  6. params[key] += self.v[key]: ここで計算した更新速度を使ってパラメータを更新します。

Momentumの実装例

Momentum最適化クラスを使用して、2次元空間のパラメータ更新のシミュレーションを行います。その後、その更新経路をグラフ化します。

# numpyとmatplotlibのインポート
import numpy as np
import matplotlib.pyplot as plt

# Momentumという名前のクラスを定義
class Momentum:

    # オブジェクトの初期化を行う__init__メソッド
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr  # 学習率
        self.momentum = momentum  # モーメンタム係数
        self.v = None  # 速度（更新量）
        
    # パラメータの更新を行うupdateメソッド
    def update(self, params, grads):
        # 初回の更新の時に速度vをパラメータと同じ形状で初期化
        if self.v is None:
            self.v = {}
            for key, val in params.items():                                
                self.v[key] = np.zeros_like(val)
        
        # 速度vとパラメータを更新
        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] 
            params[key] += self.v[key]


# 最適化対象の関数を定義
def f(x, y):
    return x**2 / 20.0 + y**2


# 最適化対象の関数の勾配を定義
def df(x, y):
    return x / 10.0, 2.0*y

# 初期位置を設定
init_pos = (-7.0, 2.0)
# 初期パラメータを設定
params = {'x': init_pos[0], 'y': init_pos[1]}
# 初期勾配を設定
grads = {'x': 0, 'y': 0}
# 最適化アルゴリズムとしてMomentumを設定
optimizer = Momentum(lr=0.1)
# パラメータの更新履歴を保存するための配列
path = np.empty((0,2))

# パラメータの更新を30回行う
for i in range(30):
    # 勾配を計算
    grads['x'], grads['y'] = df(params['x'], params['y'])
    # パラメータを更新
    optimizer.update(params, grads)
    # パラメータの更新履歴を保存
    path = np.append(path, np.array([[params['x'], params['y']]]), axis=0)

# 等高線プロットのための格子点を生成
x = np.arange(-10, 10, 0.01)
y = np.arange(-5, 5, 0.01)
X, Y = np.meshgrid(x, y) 
Z = f(X, Y)

# 等高線プロットとパラメータの更新履歴をプロット
plt.figure(figsize=(10, 7))
plt.contour(X, Y, Z, 30, cmap='jet')
plt.plot(path[:,0], path[:,1], 'o-', color='red')

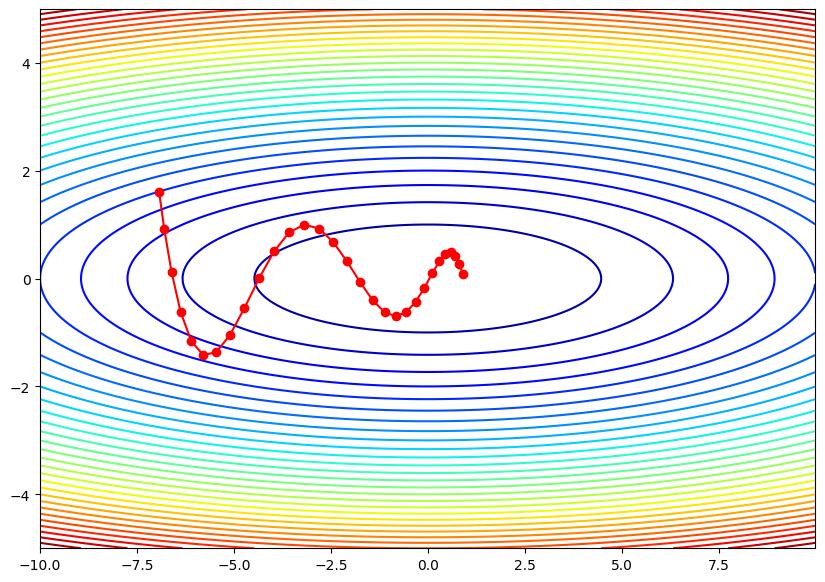
Momentumクラスは、運動量に基づくパラメータの更新を行います。__init__メソッドで学習率（lr）と運動量（momentum）を設定します。運動量とは、前回の勾配（すなわち、パラメータ更新）にある割合を掛け合わせて、今回のパラメータ更新に反映させることです。これにより、更新は加速し、極小値への収束が早まります。

updateメソッドは、パラメータ（params）と勾配（grads）を引数にとり、パラメータを更新します。初回呼び出し時には、各パラメータに対応する速度項（self.v）をゼロで初期化します。その後、速度項は前回の速度項に運動量を掛けたものと、今回の勾配に学習率を掛けたものの和として更新されます。そして、この速度項に基づいてパラメータが更新されます。

次に、関数f(x, y)とその勾配を計算するdf(x, y)を定義しています。ここでは、f(x, y)は2次元平面上のパラボラを表し、df(x, y)はその勾配を計算します。

初期位置init_posと最適化のためのMomentumオブジェクトoptimizerを作成した後、30回の更新ステップを行います。各ステップでは、まず現在のパラメータ位置における勾配を計算し、その勾配を使ってoptimizerによってパラメータを更新します。その後、更新されたパラメータ位置をpathに保存します。

まとめ

最後までご覧いただきありがとうございました。

カテゴリー
E資格、資格
タグ
前の記事
【Stable Diffusion】BRA V5で画像生成してみる【画像生成】
2023年5月30日
次の記事
【E資格まとめ】AdaGrad
2023年6月1日