このシリーズではE資格対策として、シラバスの内容を項目別にまとめています。
AdaGradの概要
基本的な最適化手法としては、確率的勾配降下法(SGD)があります。SGDでは、モデルのパラメータ(重み)を更新する際に、その勾配(すなわち、パラメータを少し変化させた時の損失関数の変化率)に基づいて更新を行います。しかし、全てのパラメータを同じように更新するため、一部のパラメータが他のパラメータに比べて勾配が大きい場合、そのパラメータの影響を過大に受けることがあります。
ここでAdaGradの出番です。AdaGrad(Adaptive Gradient)は、学習率を「適応的に」調整する手法です。それぞれのパラメータに対して、その過去の勾配の情報を使用して学習率を調整します。つまり、これまでに大きな勾配を持っていたパラメータの学習率は下げられ、小さな勾配しか持っていなかったパラメータの学習率は上げられます。これにより、各パラメータが適切な速さで学習を進められるようになります。
AdaGradの更新規則は以下の式で表されます。以下の数式を使用して、パラメータの更新方法を理解することができます。
しかしながら、AdaGradには問題もあります。訓練が進むにつれて、学習率がどんどんと小さくなってしまうという点です。これは、特に訓練データが多い場合や、訓練を長時間行う場合に問題となります。これを解決するための改良版として、RMSPropやAdamなどのアルゴリズムが提案されています。
AdaGradの実装
AdaGradの最適化アルゴリズムを実装します。
class AdaGrad:
# コンストラクタ
def __init__(self, lr=0.01):
self.lr = lr # 学習率を初期化
self.h = None # 勾配の二乗和を保存するための変数を初期化
# パラメータ更新メソッド
def update(self, params, grads):
# 初回の呼び出し時にhを初期化
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val) # 各パラメータと同じ形状のゼロ配列を生成
# 各パラメータの更新
for key in params.keys():
# 勾配の二乗を加算
self.h[key] += grads[key] * grads[key]
# AdaGradの更新式に従ってパラメータ更新
# 学習率を勾配の二乗和の平方根で割る(1e-7はゼロ除算を防ぐための微小な値)
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
まず、初期化関数__init__についてです。ここでは学習率(lr)を0.01として設定し、self.hという変数をNoneで初期化しています。このself.hは各パラメータの勾配の二乗和を保持するための変数です。
次にupdate関数について見てみましょう。この関数はパラメータ(params)と勾配(grads)を入力として受け取り、パラメータの更新を行います。
関数の最初の部分では、self.hがNone(つまり初回の呼び出し)の場合に、パラメータと同じ形状のゼロ配列を生成しています。これが各パラメータの勾配の二乗和を保持するための配列です。
その後、各パラメータについて更新を行います。まず、そのパラメータの勾配の二乗をself.h[key]に加算します。これにより、そのパラメータの過去の勾配の情報がself.h[key]に蓄積されていきます。
最後に、パラメータの更新を行います。更新量は、学習率(self.lr)と勾配(grads[key])の積を、self.h[key]の平方根で割ったものです。ここでのself.h[key]の平方根がAdaGradの特徴的な部分で、これにより過去の大きな勾配を持つパラメータの学習率が下げられ、小さな勾配しか持っていなかったパラメータの学習率が上げられます。また、割り算の際に非常に小さい値(1e-7)を足していますが、これはself.h[key]が0の場合にゼロ除算を防ぐためのものです。
AdaGradの実装例
AdaGradを用いて、2次元関数を最適化するものです。
# NumPyは数値計算を行うためのライブラリです
import numpy as np
# Matplotlibはデータの可視化を行うためのライブラリです
import matplotlib.pyplot as plt
# LogNormはカラーマップの正規化を行うためのクラスです
from matplotlib.colors import LogNorm
# AdaGradクラスの定義
class AdaGrad:
# 初期化メソッド
def __init__(self, lr=0.01):
self.lr = lr # 学習率を初期化
self.h = None # 勾配の二乗和を保存するための変数を初期化
# パラメータ更新メソッド
def update(self, params, grads):
# 初回の呼び出し時にhを初期化
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val) # 各パラメータと同じ形状のゼロ配列を生成
# 各パラメータの更新
for key in params.keys():
# 勾配の二乗を加算
self.h[key] += grads[key] * grads[key]
# AdaGradの更新式に従ってパラメータ更新
# 学習率を勾配の二乗和の平方根で割る(1e-7はゼロ除算を防ぐための微小な値)
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
# 最適化対象の関数を定義
def f(x, y):
return (1/20) * x ** 2 + y ** 2
# 関数の勾配を定義
def grad_f(x, y):
dfdx = (1/10) * x
dfdy = 2 * y
return dfdx, dfdy
# パラメータを初期化
params = {'x': -7.0, 'y': 2.0}
# AdaGradクラスのインスタンスを生成
adagrad = AdaGrad(lr=1.5)
# パラメータの更新経路を保存するためのリストを初期化
x_history = []
y_history = []
# 最適化処理
for i in range(30):
# 現在のパラメータをリストに追加
x_history.append(params['x'])
y_history.append(params['y'])
# 勾配を計算
grads = {'x': grad_f(params['x'], params['y'])[0], 'y': grad_f(params['x'], params['y'])[1]}
# パラメータを更新
adagrad.update(params, grads)
# 等高線プロットのための格子点を生成
x = np.arange(-10, 10, 0.01)
y = np.arange(-3, 3, 0.01)
X, Y = np.meshgrid(x, y)
# 関数の値を計算
Z = f(X, Y)
# 新しい図を生成
plt.figure(figsize=(12, 8))
# 等高線プロットを描画
plt.contour(X, Y, Z, levels=np.logspace(-3, 2, 35), norm=LogNorm(), cmap=plt.cm.jet)
# パラメータの更新経路を描画
plt.plot(x_history, y_history, 'ro-', linewidth=2, markersize=5)
# x軸とy軸の範囲を設定
plt.xlim(-10, 10)
plt.ylim(-3, 3)
# x軸とy軸のラベルを設定
plt.xlabel('x')
plt.ylabel('y')
# タイトルを設定
plt.title('Optimization of function using AdaGrad')
# 図を表示
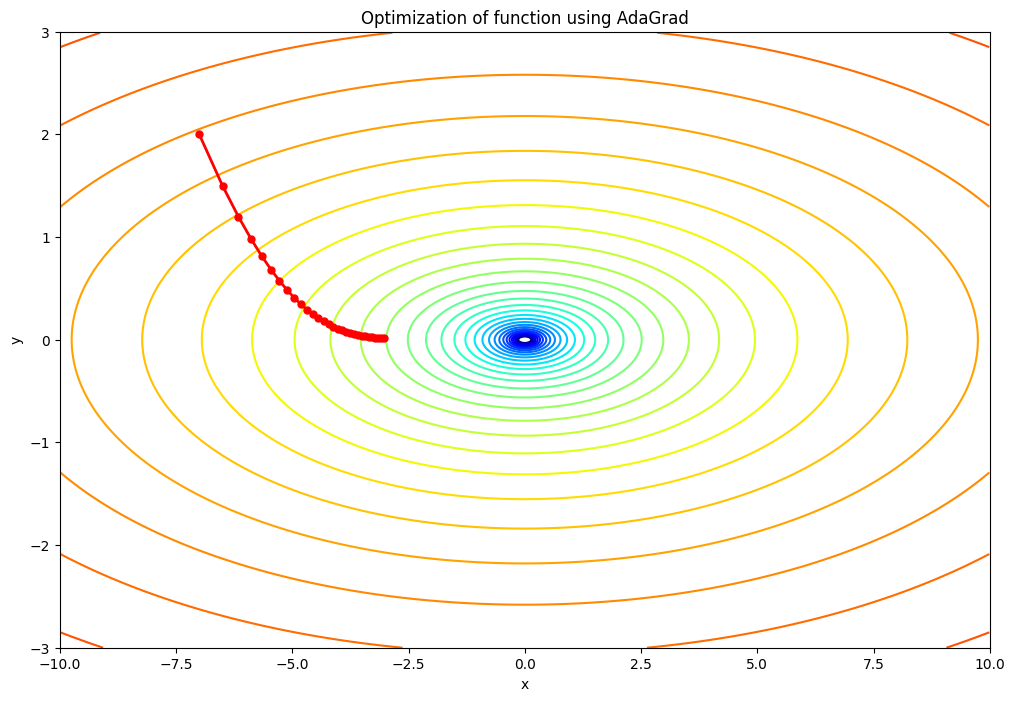
plt.show()AdaGradクラス:このクラスはAdaGradのアルゴリズムを実装しています。クラス内部にはパラメータ更新用のupdate関数が定義されており、この関数はパラメータ(params)と勾配(grads)を引数に取り、パラメータを更新します。f(x, y)関数:最適化を行いたい2次元関数を定義しています。grad_f(x, y)関数:関数fの勾配(微分)を計算するための関数です。- パラメータの初期化:パラメータ
xとyの初期値を設定し、AdaGradのインスタンスを作成しています。 - 最適化のループ:30回の繰り返しを通じてパラメータを更新しています。各ステップでは、現在のパラメータの値を履歴に保存し、勾配を計算してAdaGradによりパラメータを更新します。
- 可視化:最後に、最適化の結果をプロットするためのコードがあります。等高線プロットを使って関数
fを可視化し、赤い線でパラメータの更新履歴(最適化の過程)を描画しています。この結果から、最適化がどのように進行したかを視覚的に理解することができます。
AdaGradと学習率
lrは学習率(learning rate)を表すパラメータで、最適化アルゴリズムにおいてパラメータの更新のステップサイズを制御します。学習率の値により、最適化の振る舞いは大きく変わることがあります。
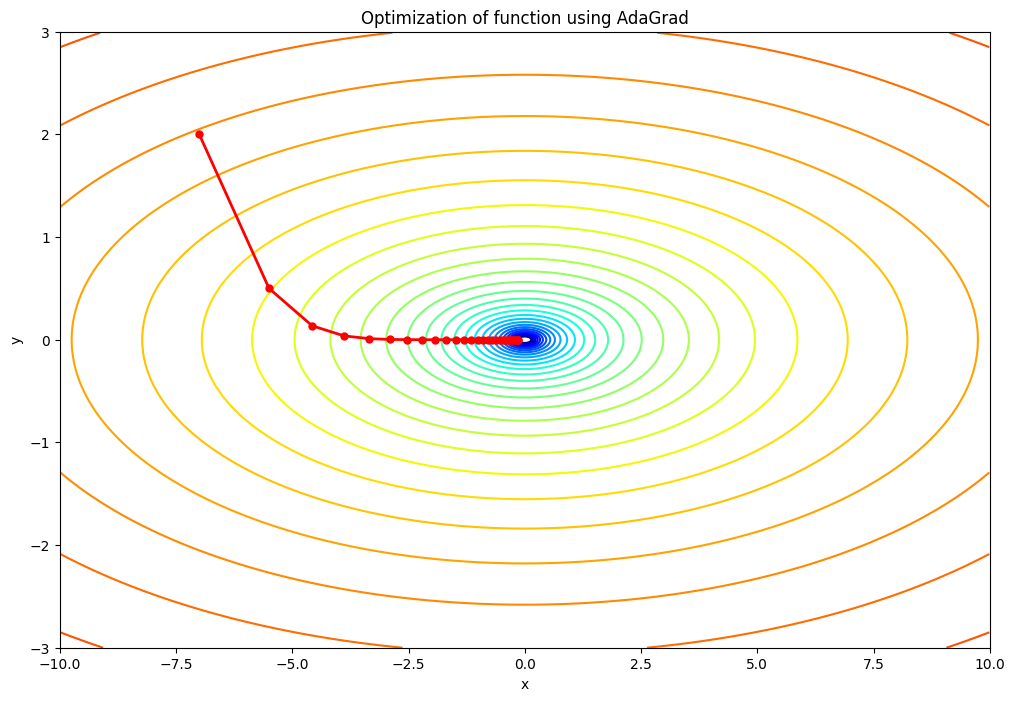
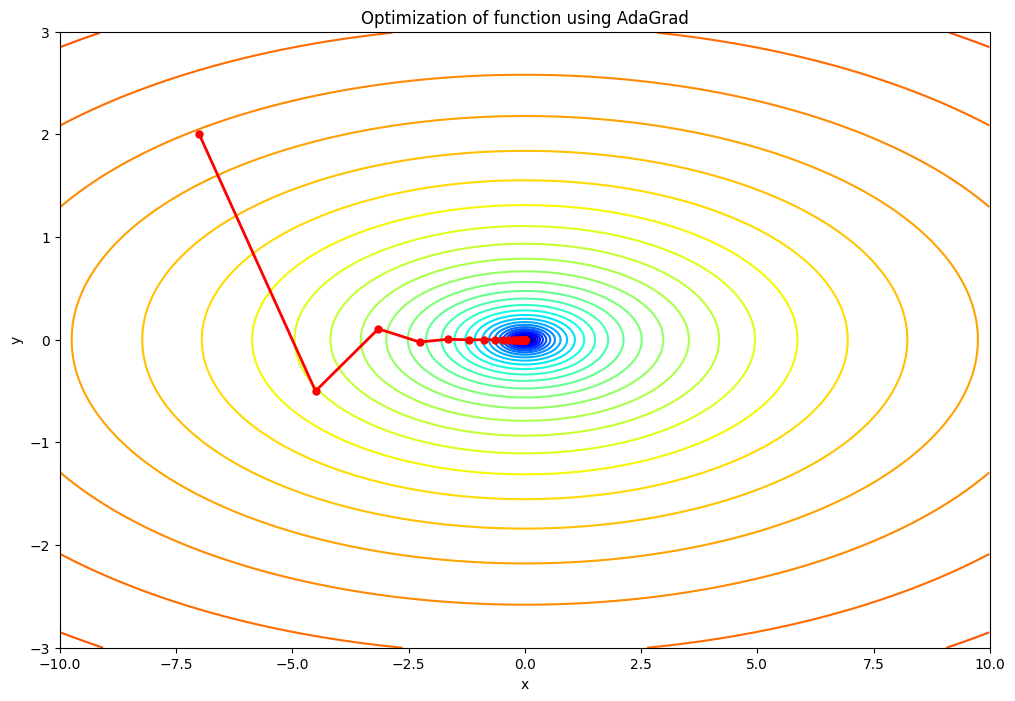
lr=0.5の場合:学習率が小さいため、パラメータの更新ステップが小さくなります。そのため、最適化のプロセスはよりゆっくりと進行し、収束するまでにより多くのイテレーションを必要とする可能性があります。ただし、学習率が小さいため、最適解を”オーバーシュート”する(つまり、最適解を通り過ぎてしまう)リスクは低いです。lr=1.5の場合:この値は元のコードの学習率と同じです。この学習率では、パラメータの更新ステップは適度な大きさとなり、適切な数のイテレーションで収束すると期待されます。lr=2.5の場合:学習率が大きいため、パラメータの更新ステップも大きくなります。その結果、最適化のプロセスはより速く進行し、少ないイテレーションで収束する可能性があります。ただし、学習率が大きすぎると、最適解をオーバーシュートするリスクが高まり、最適化が不安定になる可能性があります。つまり、最適解を通り過ぎてしまい、反対側に大きく跳ね返るような挙動を示すことがあります。
まとめ
最後までご覧いただきありがとうございました。
