このシリーズではE資格対策として、シラバスの内容を項目別にまとめています。
E資格まとめ
試験概要 ディープラーニングの理論を理解し、適切な手法を選択して実装する能力や知識を有しているかを認定する。 １．応用数学 （１）確率・統計 （２）情報理論 ２．機…
つくもちブログ 〜Python&AIまとめ〜 RMSpropの概要
RMSpropの概要
RMSpropは、Adagradアルゴリズムの問題を解決するために提案されました。Adagradは勾配の二乗の累積和を使用して、学習率を調整しますが、学習が進むにつれて学習率が急速に小さくなることがあります。この問題を解決するために、RMSpropは勾配の二乗の移動平均を使用して、過去の勾配の影響を減らすように設計されました。
- 移動平均の計算: 前回の移動平均と現在の勾配の二乗から、新しい移動平均を計算します。
- パラメータの更新: 移動平均を使用して、各パラメータの学習率を調整し、パラメータを更新します。
RMSpropの更新規則は以下の数式で表されます。
\begin{align}
h_t & = \text{decay_rate} \cdot h_{t-1} + (1 – \text{decay_rate}) \cdot (g_t)^2 \\
\theta_t & = \theta_{t-1} – \frac{{\text{{lr}} \cdot g_t}}{{\sqrt{{h_t}} + \epsilon}}
\end{align}
学習率（lr）: 学習の速度を制御します。大きすぎると学習が不安定になり、小さすぎると学習が遅くなります。
減衰率（decay_rate）: 勾配の二乗の移動平均の減衰度を制御します。通常、0.9から0.99の間の値が使用されます。
RMSpropの特徴
- 自動学習率調整: RMSpropは各パラメータに対して個別の学習率を計算します。これにより、パラメータごとに最適な学習率が適用されるため、効率的な学習が可能です。
- 勾配の二乗の移動平均: 過去の勾配の情報を指数移動平均で取り入れます。これによって、過去の勾配の影響を適切にコントロールでき、学習の安定性が向上します。
- 学習率の急減少の回避: Adagradの問題である学習率の急激な減少を回避し、学習の途中で学習率が0に近づきすぎる問題を解決します。
RMSpropの利点
効率的な学習: 学習率の自動調整により、各パラメータが最適な速度で更新されるため、学習が効率的に行えます。
学習の安定化: 移動平均による勾配の平滑化と学習率の適切な調整により、学習プロセスが安定します。
ハイパーパラメータの柔軟性: 減衰率（decay_rate）などのハイパーパラメータは、多くの問題に対して同じ値で効果的であることが多いため、ハイパーパラメータのチューニングが容易です。
スケールの異なるパラメータへの対応: 各パラメータに対して異なる学習率が適用されるため、スケールが大きく異なるパラメータでも適切に学習が進行します。
RMSpropの実装
# 必要なライブラリをインポート
import numpy as np
import matplotlib.pyplot as plt
class RMSprop:
def __init__(self, lr=0.01, decay_rate=0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
# 目的関数の定義
def f(x, y):
return (1/20) * x**2 + y**2
# 目的関数の勾配の定義
def gradient_f(x, y):
return np.array([x/10, 2*y])
# RMSpropオプティマイザのインスタンスを作成
optimizer = RMSprop(lr=0.3)
# パラメータの初期化
params = {"x": -7.0, "y": 2.0}
# 最適化の経路を保存するためのリスト
path = [(params["x"], params["y"])]
# 最適化ループ
for i in range(30):
# 勾配の計算
grads = {"x": gradient_f(params["x"], params["y"])[0], "y": gradient_f(params["x"], params["y"])[1]}
# パラメータの更新
optimizer.update(params, grads)
# 現在のパラメータの値を経路に追加
path.append((params["x"], params["y"]))
# 経路をnumpy配列に変換
path = np.array(path)
# 表示用のxとyの値を生成
x = np.arange(-10, 10, 0.1)
y = np.arange(-5, 5, 0.1)
X, Y = np.meshgrid(x, y)
# Zを計算するために目的関数を適用
Z = f(X, Y)
# プロットの初期化
plt.figure(figsize=(10, 8))
# 目的関数の等高線をプロット
plt.contour(X, Y, Z, levels=np.logspace(-2, 2, 20))
# パラメータの更新経路をプロット
plt.plot(path[:,0], path[:,1], 'o-', color='red')
# x軸のラベルを設定
plt.xlabel('x')
# y軸のラベルを設定
plt.ylabel('y')
# タイトルを設定
plt.title('RMSprop Optimization')
# グリッドを表示
plt.grid()
# プロットを表示
plt.show()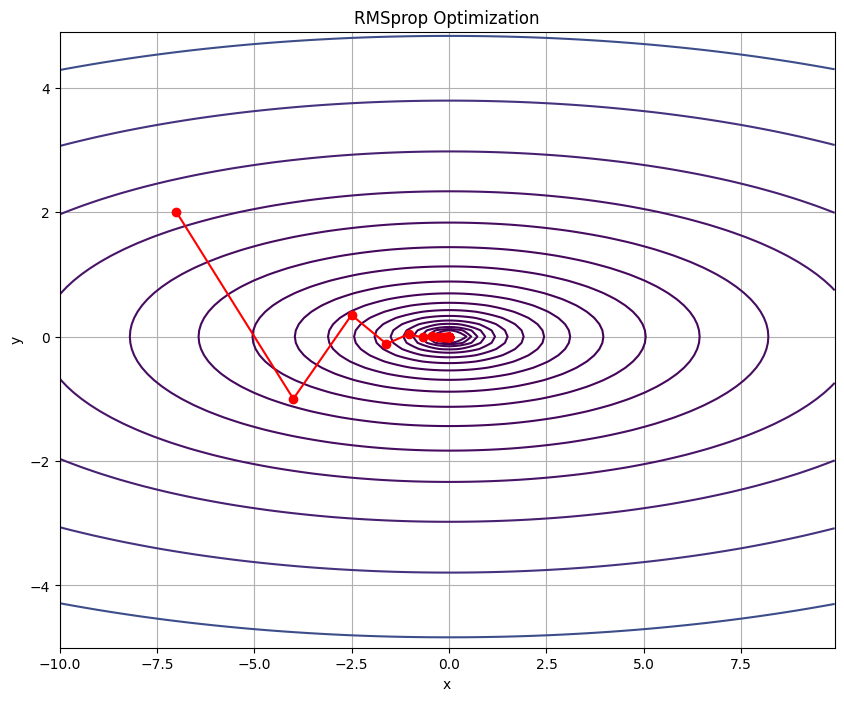
まとめ
最後までご覧いただきありがとうございました。
