このシリーズではE資格対策として、シラバスの内容を項目別にまとめています。
プーリング層(Pooling Layer)
プーリング層(Pooling Layer)
プーリング層(Pooling Layer)は、主に畳み込みニューラルネットワーク(CNN)において使用される層で、特徴マップの次元を削減するために用います。これにより、計算量を減らし、モデルの過学習を防ぐ効果があります。
プーリング層の主な種類には次の2つがあります。
- マックスプーリング層(Max Pooling)
- アベレージプーリング(Average Pooling)
マックスプーリング層(Max Pooling)
最大プーリングは、畳み込みニューラルネットワークのプーリング層においてよく用いられる操作で、特定の領域内で最大の値を選ぶ操作です。特徴マップの次元削減と重要な特徴の抽出に役立ちます。特定の領域内で最大の値を選ぶことで、モデルの計算量を削減し、過学習を防ぐ効果があります。特に、畳み込みニューラルネットワークにおいて重要な役割を果たします。
- 入力特徴マップを一定のサイズ(例: 2×2)のウィンドウに分割します。
- 各ウィンドウ内で最大の値を取り出します。
- これらの最大値を用いて新しい特徴マップを構築します。
この操作によって、特徴マップのサイズが削減され、計算量が減少します。さらに、最も重要な特徴だけを残すことで、モデルがロバストになる効果も期待されます。
マックスプーリング層は、特定の領域内で最大の値を選ぶ操作です。以下の数式で表されます。
$$
\text{MaxPooling}(X) = \max(X_{i, j})
$$
アベレージプーリング(Average Pooling)
アベレージプーリングは、マックスプーリングと同様に、特定の領域内の値を一つにまとめる操作ですが、マックスプーリングが最大値を選ぶのに対し、アベレージプーリングは平均値を計算します。
作用のメカニズム
- 入力特徴マップを一定のサイズ(例: 2×2)のウィンドウに分割します。
- 各ウィンドウ内の値の平均を計算します。
- これらの平均値を用いて新しい特徴マップを構築します。
この操作によって、特徴マップのサイズが削減されるだけでなく、領域内の全ての情報を均等に取り入れるため、特徴の偏りを抑制する効果があります。
アベレージプーリングは、特定の領域内の値の平均を計算する操作です。以下の数式で表されます。
$$
\text{AveragePooling}(X) = \frac{{\sum(X_{i, j})}}{{n}}
$$
マックスプーリング層の実装
# NumPyライブラリのインポート
import numpy as np
# 1x1x4x4のランダムな配列を生成
x = np.random.rand(1, 1, 4, 4)
# プーリング層のクラス定義
class Pooling:
# コンストラクタ: プーリング層のパラメータを初期化
def __init__(self, pool_h, pool_w, stride=2, pad=0):
self.pool_h = pool_h # プーリング領域の高さ
self.pool_w = pool_w # プーリング領域の幅
self.stride = stride # ストライド
self.pad = pad # パディング
self.x = None # 入力データ
self.arg_max = None # 最大値のインデックス
# 順伝播メソッド
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
# im2colを用いて、入力データを2次元配列に変換
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h*self.pool_w)
# 最大値とそのインデックスを取得
arg_max = np.argmax(col, axis=1)
out = np.max(col, axis=1)
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
self.x = x
self.arg_max = arg_max
return out
# 逆伝播メソッド
def backward(self, dout):
dout = dout.transpose(0, 2, 3, 1)
pool_size = self.pool_h * self.pool_w
dmax = np.zeros((dout.size, pool_size))
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
dmax = dmax.reshape(dout.shape + (pool_size,))
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
return dx
# im2col関数: 画像データを2次元配列に変換
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
N, C, H, W = input_data.shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
# col2im関数: 2次元配列を画像データに変換
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
N, C, H, W = input_shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)
img = np.zeros((N, C, H + 2*pad + stride - 1, W + 2*pad + stride - 1))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]
return img[:, :, pad:H + pad, pad:W + pad]
# プーリング層のパラメータ設定
pool_h = 2
pool_w = 2
stride = 2
pad = 0
# プーリング層のインスタンス生成
pooling_layer = Pooling(pool_h, pool_w, stride, pad)
# 順伝播の実行
out = pooling_layer.forward(x)
# 入力と出力の表示
print("Input:")
print(x)
print("Output:")
print(out)
実行結果:
Input:
[[[[0.48292004 0.50898482 0.25630539 0.33505258]
[0.34845638 0.68695185 0.88556479 0.89610986]
[0.37071103 0.84248171 0.18418369 0.74160331]
[0.59484312 0.51291107 0.14409389 0.68989917]]]]
Output:
[[[[0.68695185 0.89610986]
[0.84248171 0.74160331]]]]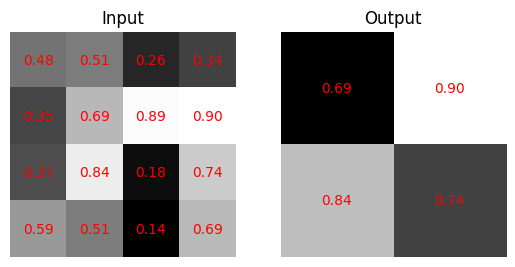
まとめ
最後までご覧いただきありがとうございました。