このシリーズではE資格対策として、シラバスの内容を項目別にまとめています。
Adamとは
Adam(Adaptive Moment Estimation)は、最適化手法の一つで、機械学習モデルが学習する際に、より効率的にパラメータを更新するためのアルゴリズムです。
Adamは、それぞれ異なるアイデアを組み合わせたアルゴリズムで、その2つの主要なアイデアは「Momentum」(運動量)と「AdaGrad」(適応的勾配)です。
まず、「Momentum」について説明します。これは物理の概念を借りたもので、運動量がある物体が、勾配(山や谷)を下るときに速度が上がるというアイデアを使います。つまり、パラメータ更新の方向が一貫している場合(つまり、同じ方向にパラメータを更新し続ける場合)、更新の速度が徐々に上がるということです。これにより、最適な解に早く近づけるようになります。
次に、「AdaGrad」について説明します。AdaGradは、学習率(パラメータ更新のスピードを決めるパラメータ)を自動的に調整することで、学習プロセスを改善しようとするアイデアです。特定のパラメータが頻繁に更新される場合、AdaGradはそのパラメータの学習率を下げます。逆に、あまり更新されないパラメータは、学習率が上がります。これにより、全体の学習プロセスが均一化され、最適な解に早く到達します。
つまり、Adamはパラメータの更新方向とスピードを同時に考慮し、より効率的に学習を進めることを可能にします。パラメータ更新の方向が一貫している場合(つまり、同じ方向にパラメータを更新し続ける場合)は、更新の速度が徐々に上がり(これがMomentumの効果)、特定のパラメータが頻繁に更新される場合は、そのパラメータの学習率を下げます(これがAdaGradの効果)。
さらに、Adamは過去の勾配の二乗の移動平均(これが「モーメント」と呼ばれる)を保持することで、学習率を各パラメータに対して適応的に調整します。これにより、各パラメータの学習率がデータのスケールに適応的になり、より堅牢な学習が可能になります。
Adamの実装
Adamの最適化アルゴリズムを実装します。
# Adam クラスの定義
class Adam:
# インスタンス化時に学習率(lr), 一次モーメントの係数(beta1), 二次モーメントの係数(beta2)を初期設定
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr # 学習率
self.beta1 = beta1 # 一次モーメント推定に使用する係数
self.beta2 = beta2 # 二次モーメント推定に使用する係数
self.iter = 0 # イテレーションのカウント
self.m = None # 一次モーメント(移動平均)
self.v = None # 二次モーメント(移動分散)
# パラメータの更新メソッド
def update(self, params, grads):
# 最初の更新時に一次モーメントと二次モーメントの格納用の辞書をパラメータと同じ形で初期化
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val) # 一次モーメント用の辞書
self.v[key] = np.zeros_like(val) # 二次モーメント用の辞書
# イテレーション数をカウントアップ
self.iter += 1
# 学習率の時間的なスケーリング(Adamのバイアス補正)
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
# 各パラメータについて
for key in params.keys():
# 一次モーメント(過去の勾配の減衰平均)を更新
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
# 二次モーメント(過去の勾配の二乗の減衰平均)を更新
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
# 勾配によるパラメータの更新(Adamの更新式)
# 二次モーメントの平方根(+微小値でゼロ除算を防ぐ)で一次モーメントをスケーリングし、学習率をかけてパラメータを更新
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
__init__(self, lr=0.001, beta1=0.9, beta2=0.999): 初期化メソッドで、Adamのハイパーパラメータ(学習率lr、勾配の平均の減衰率beta1、勾配の2乗の平均の減衰率beta2)を設定します。また、self.iterでAdamの更新回数を保持し、self.mとself.vで1次モーメント(平均)と2次モーメント(分散)を保持します。update(self, params, grads): パラメータを更新するメソッドです。入力paramsは更新するパラメータの辞書、gradsはそれぞれのパラメータの勾配の辞書です。まず、初回実行時にself.mとself.vをパラメータと同じ形のゼロで初期化します。その後、Adamの更新ルールに従ってパラメータを更新します。具体的には、各パラメータに対して、まず1次モーメント(平均)と2次モーメント(分散)を更新し、それらを用いてパラメータを更新します。
このコードの最後の部分params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)では、Adamの更新ルールに従い、パラメータを更新しています。ここで、1e-7はゼロ除算を防ぐための小さな値(通常「イプシロン」または「epsilon」と呼ばれる)です。
Adamの実装例
Adamを用いて、2次元関数を最適化するものです。
# 必要なライブラリをインポート
import numpy as np
import matplotlib.pyplot as plt
# Adamオプティマイザのクラスを定義
class Adam:
# 初期化メソッド
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr # 学習率
self.beta1 = beta1 # モーメンタムの係数
self.beta2 = beta2 # RMSpropの係数
self.iter = 0 # イテレーション数の初期化
self.m = None # モーメンタムの初期化
self.v = None # RMSpropの初期化
# パラメータの更新メソッド
def update(self, params, grads):
# mとvが初期化されていない場合、それらをパラメータと同じ形状で初期化する
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
# イテレーション数を増やす
self.iter += 1
# 学習率の更新(Adamの特性により、イテレーションの進行とともに学習率が調整される)
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
# 各パラメータに対して更新を行う
for key in params.keys():
# モーメンタムの計算
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
# RMSpropの計算
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
# パラメータの更新
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
# 目的関数の定義
def f(x, y):
return (1/20) * x**2 + y**2
# 目的関数の勾配の定義
def gradient_f(x, y):
return np.array([x/10, 2*y])
# Adamオプティマイザのインスタンスを作成
optimizer = Adam(lr=0.3)
# パラメータの初期化
params = {"x": -7.0, "y": 2.0}
# 最適化の経路を保存するためのリスト
path = [(params["x"], params["y"])]
# 最適化ループ
for i in range(30):
# 勾配の計算
grads = {"x": gradient_f(params["x"], params["y"])[0], "y": gradient_f(params["x"], params["y"])[1]}
# パラメータの更新
optimizer.update(params, grads)
# 現在のパラメータの値を経路に追加
path.append((params["x"], params["y"]))
# 経路をnumpy配列に変換
path = np.array(path)
# 表示用のxとyの値を生成
x = np.arange(-10, 10, 0.1)
y = np.arange(-5, 5, 0.1)
X, Y = np.meshgrid(x, y)
# Zを計算するために目的関数を適用
Z = f(X, Y)
# プロットの初期化
plt.figure(figsize=(10, 8))
# 目的関数の等高線をプロット
plt.contour(X, Y, Z, levels=np.logspace(-2, 2, 20))
# パラメータの更新経路をプロット
plt.plot(path[:,0], path[:,1], 'o-', color='red')
# x軸のラベルを設定
plt.xlabel('x')
# y軸のラベルを設定
plt.ylabel('y')
# タイトルを設定
plt.title('Adam Optimization')
# グリッドを表示
plt.grid()
# プロットを表示
plt.show()
- Adamクラスの定義: このクラスはAdam最適化アルゴリズムの実装です。初期化メソッド
__init__では、学習率(lr)とモーメンタムの係数(beta1とbeta2)を受け取り、内部的なカウンター(iter)と、各パラメータの勾配の移動平均(m)とその二乗の移動平均(v)を初期化します。updateメソッドでは、現在のパラメータ値とその勾配を受け取り、Adamのアルゴリズムに従ってパラメータを更新します。 - 関数fとその勾配の定義: ここでは、最適化したい関数
fとその勾配を計算する関数gradient_fを定義しています。これらは、Adamが最小化するべき目的関数とその勾配です。 - 最適化の初期化と実行: Adamオプティマイザーのインスタンスを作成し、最初のパラメータ値を
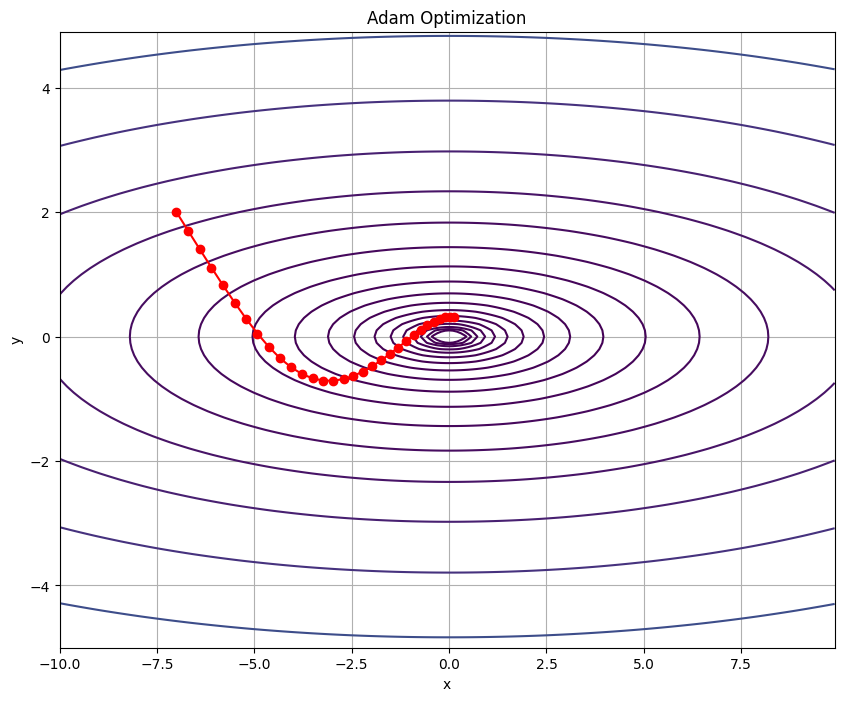
paramsに設定します。次に、30回のイテレーションを行い、各ステップで勾配を計算し、それを使ってパラメータを更新します。更新されたパラメータは、pathリストに追加されて記録されます。 - 結果の視覚化: 最後に、matplotlibを使って関数
fの等高線と、最適化の経路(path)をプロットしています。これにより、Adamがどのようにして最小値を探し出すかを視覚的に理解することができます。
まとめ
最後までご覧いただきありがとうございました。
