このシリーズではE資格対策として、書籍「ゼロから作るDeep Learning」を参考に学習に役立つ情報をまとめています。
<参考書籍>
全結合層と畳み込み層
全結合層(Affineレイヤ)と畳み込み層(Convolutionレイヤ)は、ニューラルネットワークの中で異なる役割を果たします。それぞれの特性と違いについて詳しく解説します。
全結合層(Affineレイヤ): 全結合層は、ニューラルネットワークの各層のすべてのニューロンが、前の層のすべてのニューロンと接続されている層です。これは、各入力特徴が出力にどのように影響するかを学習するために使用されます。全結合層は、入力と重みの内積を計算し、バイアスを加えることで動作します。ReLU(Rectified Linear Unit)は一般的な活性化関数で、非線形性を導入し、ネットワークがより複雑なパターンを学習するのを助けます。ReLUは、負の入力に対しては0を出力し、正の入力に対してはそのままの値を出力します。
畳み込み層(Convolutionレイヤ): 畳み込み層は、主に画像や音声などのグリッド状のデータを処理するために使用される特殊な種類の層です。畳み込み層は、小さな領域(フィルターまたはカーネルと呼ばれる)をスライドさせて入力全体に適用し、特徴マップを生成します。これにより、ネットワークは空間的な構造を学習し、位置に関係なく特徴を検出することができます。畳み込み層は、フィルターの重みとバイアスを学習します。
全結合層と畳み込み層の違い
全結合層と畳み込み層の主な違いは、全結合層がデータの空間的な構造を無視するのに対し、畳み込み層はその構造を利用することです。全結合層は入力をフラットなベクトルとして扱いますが、畳み込み層は入力の形状(例えば、画像の場合は高さ、幅、チャンネル)を保持します。これにより、畳み込み層は特に画像などの空間的な構造を持つデータに対して有効です。
また、畳み込み層はパラメータの共有(同じフィルターを入力の異なる部分に適用)を行うため、全結合層と比較してパラメータの数が大幅に少なくなります。これは計算効率を向上させ、過学習を防ぐ助けとなります。
さらに、畳み込み層は局所的な特徴を捉える能力があります。つまり、小さな領域内でのパターンや特徴を検出することができます。これは、画像のようなデータでは非常に有用です。なぜなら、画像の一部に存在する特徴(たとえば、エッジやテクスチャ)が、画像の他の部分でも同様に重要である可能性が高いからです。
一方、全結合層は、入力特徴全体を考慮して出力を生成します。これは、入力特徴間の相互作用や依存関係を捉えるのに有用です。しかし、このアプローチは、パラメータの数が多くなるため、計算コストが高くなり、過学習のリスクが増えます。
畳み込み演算
畳み込み演算(Convolution)は、一部分の情報を全体に適用する一種の数学的操作です。フィルタ(またはカーネル)と呼ばれる小さな行列が用いられ、このフィルタが信号上を移動(「スライド」)しながら、その各部分との要素ごとの積の和(ドット積)を計算します。
以下に4×4の画像と3×3のフィルタによる畳み込み演算の例を示します。
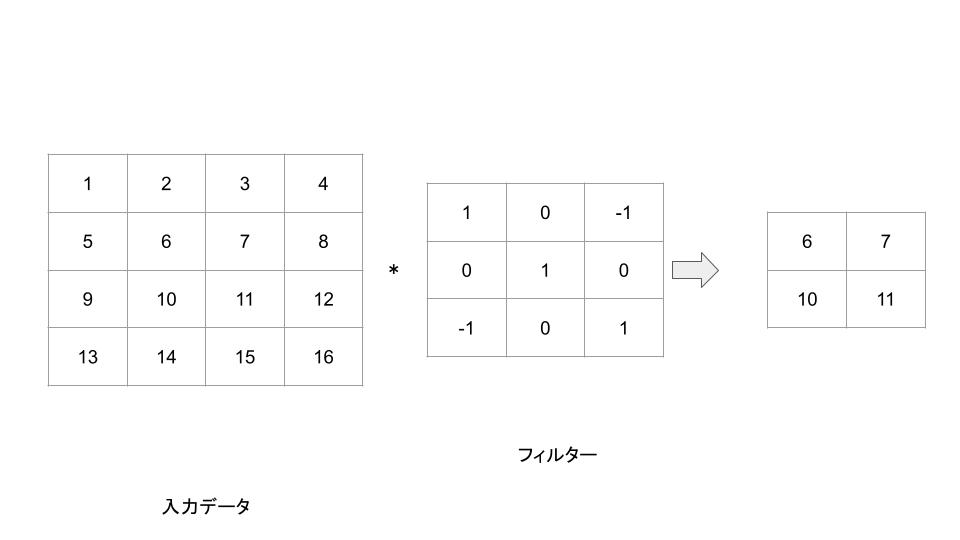
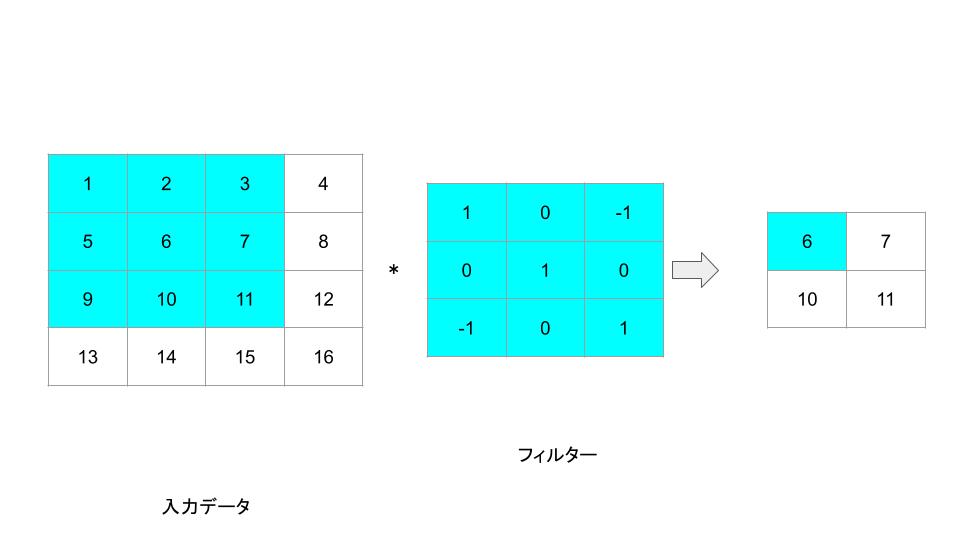
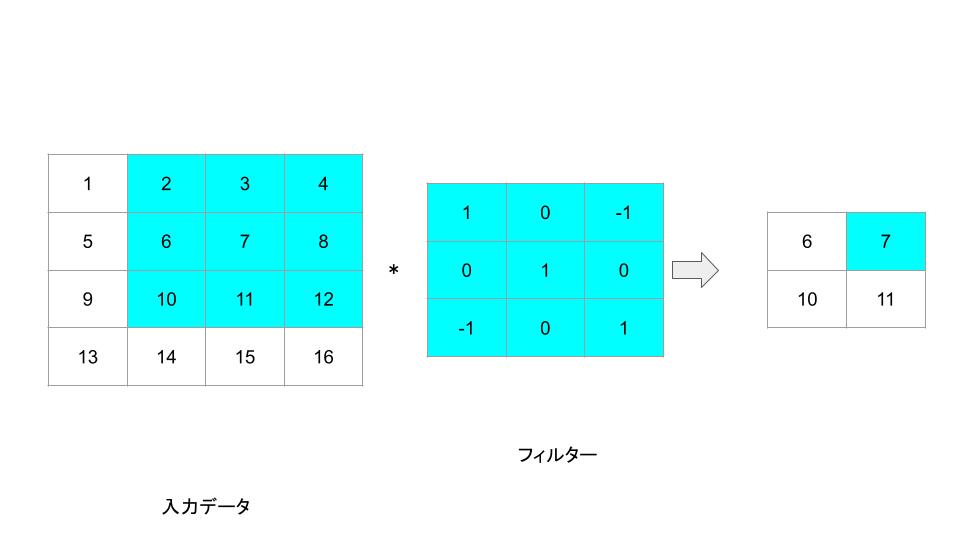
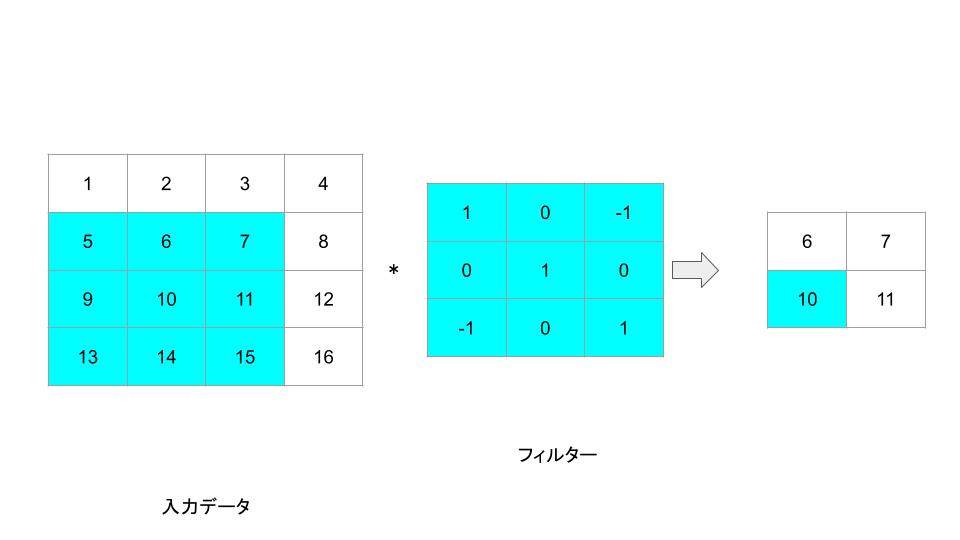
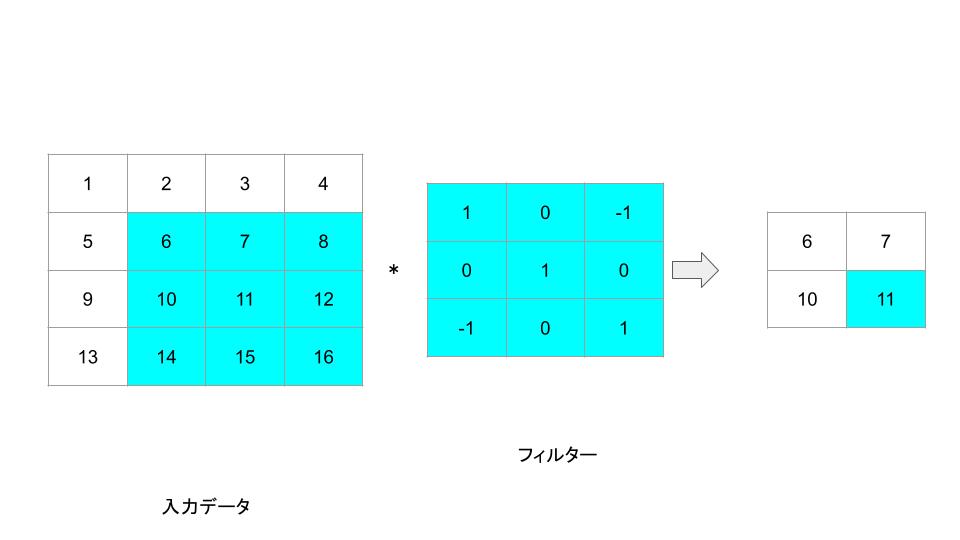
これらを用いて畳み込み演算を行うと、新しい2×2の出力画像が生成されます。各要素は元の画像の対応する部分とフィルタを要素ごとに掛け合わせ、その和を計算したものになります。
この例は非常に単純化されていますが、このような操作を用いて実際の畳み込みニューラルネットワークでは、画像から特徴を抽出します。また、通常の畳み込みニューラルネットワークでは、複数のフィルタを同時に使用し、それぞれの結果をスタックします。これにより、ネットワークは画像の異なる特徴(エッジ、色、テクスチャなど)を同時に学習することができます。
Pythonでの実装コードは以下のようになります。
import numpy as np
# 2次元配列 (4x4)
a = np.array([
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12],
[13, 14, 15, 16]
])
# 畳み込みを行うカーネル (3x3)
kernel = np.array([
[1, 0, -1],
[0, 1, 0],
[-1, 0, 1]
])
# 入力配列とカーネルのサイズ
n, m = a.shape
kn, km = kernel.shape
# 畳み込み結果を格納する配列 (n-kn+1)x(m-km+1)
result = np.zeros((n - kn + 1, m - km + 1))
# 畳み込み演算
for i in range(result.shape[0]):
for j in range(result.shape[1]):
result[i, j] = np.sum(a[i:i+kn, j:j+km] * kernel)
print(result)実行結果:
[[ 6. 7.]
[10. 11.]]まとめ
最後までご覧いただきありがとうございました。
