このシリーズではE資格対策として、書籍「ゼロから作るDeep Learning」を参考に学習に役立つ情報をまとめています。
<参考書籍>
Weight decayの概要
Weight Decayはニューラルネットワークの訓練中に適用される正則化手法の一つで、モデルの過学習(Overfitting)を防ぐ役割を果たします。Weight Decayではモデルの重みが大きくなりすぎないように、損失関数に重みの大きさに比例する項を追加します。具体的には、重みの二乗ノルム(L2ノルム)を損失関数に加えることが一般的です。
メリット
- 過学習の抑制:Weight Decayは大きな重みにペナルティを課すため、モデルが訓練データに過度に適合することを防ぎます。これにより、モデルの汎化性能が向上します。
- モデルの簡略化:大きな重みを持つパラメータにペナルティを課すことで、モデルの複雑さを制限します。これにより、モデルが必要以上に複雑になることを防ぐことができます。
デメリット
- ハイパーパラメータの調整:Weight Decayの効果は、重み減衰項の大きさを制御するハイパーパラメータにより決定されます。このハイパーパラメータの適切な設定は問題依存であり、調整が難しい場合があります。
- 適用範囲:Weight Decayは全てのパラメータに等しく適用されますが、すべてのパラメータが等しく重要であるわけではないため、必ずしも最適な正則化手法とは限りません。例えば、一部の特徴が他の特徴よりも重要な場合、L1正則化(Lasso)の方が適しているかもしれません。
Weight decayの実装
ニューラルネットワークのモデルを学習する際にWeight Decay(重み減衰)という手法を用いています。Weight Decayは過学習(overfitting)を防ぐための正則化(regularization)の一種であり、大きな重みに対してペナルティを与えることでモデルの複雑さを抑え、汎化性能を向上させます。
以下にこのコードのWeight Decayの部分を具体的に解説します。
このコードの以下の部分で、重み減衰項(Weight Decay)の計算が行われています。
def loss(self, x, t):
y = self.predict(x)
weight_decay = 0
for idx in range(1, self.hidden_layer_num + 2):
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
return self.last_layer.forward(y, t) + weight_decayここで、weight_decay_lambdaはWeight Decayの強さを決定するハイパーパラメータで、全ての重み行列Wについてその全ての要素の二乗和を計算し、その合計にweight_decay_lambdaを乗じたものがWeight Decayによる損失の増分となります。この計算結果を元の損失に加算することで、大きな重みほど大きなペナルティがかかるようにしています。
その後、逆伝播法による勾配の計算では、この重み減衰項も考慮することで、重みが適切に更新されます。
実装(MNIST)
MNISTによる多クラス分類を実装します。
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
class MultiLayerNet:
def __init__(self, input_size, hidden_size_list, output_size,
activation='relu', weight_init_std='relu', weight_decay_lambda=0):
self.input_size = input_size
self.output_size = output_size
self.hidden_size_list = hidden_size_list
self.hidden_layer_num = len(hidden_size_list)
self.weight_decay_lambda = weight_decay_lambda
self.params = {}
self.__init_weight(weight_init_std)
activation_layer = {'sigmoid': Sigmoid, 'relu': Relu}
self.layers = OrderedDict()
for idx in range(1, self.hidden_layer_num+1):
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)])
self.layers['Activation_function' + str(idx)] = activation_layer[activation]()
idx = self.hidden_layer_num + 1
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)])
self.last_layer = SoftmaxWithLoss()
def __init_weight(self, weight_init_std):
all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
for idx in range(1, len(all_size_list)):
scale = weight_init_std
if str(weight_init_std).lower() in ('relu', 'he'):
scale = np.sqrt(2.0 / all_size_list[idx - 1])
elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
scale = np.sqrt(1.0 / all_size_list[idx - 1])
self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx])
self.params['b' + str(idx)] = np.zeros(all_size_list[idx])
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
weight_decay = 0
for idx in range(1, self.hidden_layer_num + 2):
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
return self.last_layer.forward(y, t) + weight_decay
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1 : t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
for idx in range(1, self.hidden_layer_num+2):
grads['W' + str(idx)] = numerical_gradient(loss_W, self.params['W' + str(idx)])
grads['b' + str(idx)] = numerical_gradient(loss_W, self.params['b' + str(idx)])
return grads
def gradient(self, x, t):
self.loss(x, t)
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
grads = {}
for idx in range(1, self.hidden_layer_num+2):
grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.layers['Affine' + str(idx)].W
grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db
return grads
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = sigmoid(x)
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
class Affine:
def __init__(self, W, b):
self.W =W
self.b = b
self.x = None
self.original_x_shape = None
self.dW = None
self.db = None
def forward(self, x):
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape)
return dx
class SoftmaxWithLoss:
def __init__(self):
self.loss = None
self.y = None
self.t = None
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
if self.t.size == self.y.size:
dx = (self.y - self.t) / batch_size
else:
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx = dx / batch_size
return dx
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
def softmax(x):
x = x - np.max(x, axis=-1, keepdims=True)
return np.exp(x) / np.sum(np.exp(x), axis=-1, keepdims=True)
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
# 必要なライブラリをインポートします
from keras.datasets import mnist
# MNISTデータセットをロードし、訓練データとテストデータに分けます
(x_train, t_train), (x_test, t_test) = mnist.load_data()
# データを前処理します(255で除算して0から1の範囲に正規化します)
x_train, x_test = x_train / 255.0, x_test / 255.0
# 訓練データを300までに制限します
x_train = x_train[:300]
t_train = t_train[:300]
# 重み減衰のパラメータを設定します
weight_decay_lambda = 0.1
# ネットワーク(多層パーセプトロン)を作成します
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
weight_decay_lambda=weight_decay_lambda)
# 最適化手法を選択します(ここでは確率的勾配降下法を使用します)
optimizer = SGD(lr=0.01)
# エポック数の最大値を設定します
max_epochs = 201
# 訓練データのサイズを取得します
train_size = x_train.shape[0]
# バッチサイズを設定します
batch_size = 100
# 訓練とテストの精度と損失を記録するリストを初期化します
train_loss_list = []
train_acc_list = []
test_acc_list = []
# エポックごとの反復回数を計算します
iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0
# 指定された反復回数まで訓練を行います
for i in range(1000000000):
# バッチデータを取得します
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 勾配を計算します
grads = network.gradient(x_batch, t_batch)
# パラメータを更新します
optimizer.update(network.params, grads)
# 各エポックの終わりに精度を評価します
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("epoch:" + str(epoch_cnt) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc))
epoch_cnt += 1
if epoch_cnt >= max_epochs:
break
# 訓練とテストの精度をプロットします
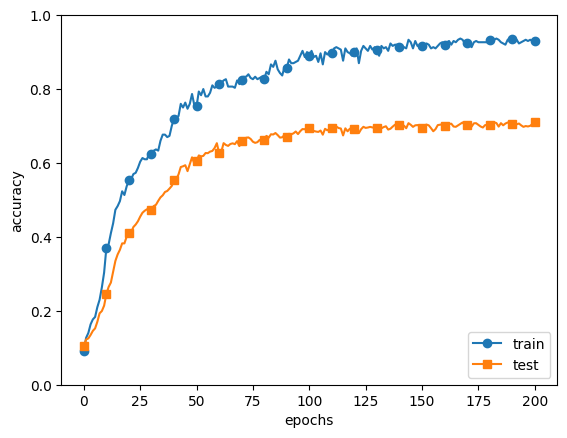
markers = {'train': 'o', 'test': 's'}
x = np.arange(max_epochs)
plt.plot(x, train_acc_list, marker='o', label='train', markevery=10)
plt.plot(x, test_acc_list, marker='s', label='test', markevery=10)
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
まとめ
最後までご覧いただきありがとうございました。

